Statistical Good Practice Guidelines

Modern Approaches to the Analysis of Experimental Data

Release date: January 2001

This is one of a series of guides for research and support staff involved in natural resources projects. The subject-matter here is modern approaches to the analysis of experimental data. Other guides give information on allied topics. Your comments on any aspect of the guides would be welcomed.

 

Acknowledgements

This guide has been developed from a course on the analysis of experimental data that has been prepared jointly by the Statistical Services Centre and ICRAF. These guidelines give the key points. The full course notes and examples are available on CD or from the Web sites at Reading or ICRAF in both English and French.

The approach used in this guide and in the corresponding training courses has been tested in English in a regional course in Nairobi and in French in national training courses in Benin and Guinea. It appears to be constructive in giving scientists the skills to recognise the types of approach needed for the analysis of their data and the confidence to proceed with the analysis even if there are complications in the data.

Preamble

Many researchers have attended a statistics course at some time in their lives, but still find some aspects of statistics confusing, particularly in relation to the analysis of their own data. Here we show that simple presentations can often satisfy most of the objectives of a research study. These are easy to undertake by all scientists. This approach also clarifies the extra information that is provided by an Analysis of Variance (ANOVA) and by the use of standard statistical models.

We contrast this approach with the "automatic" attitude to analysis that is sometimes used by scientists who are not comfortable with statistics. Their approach is characterised by the blanket statement that the data will be "analysed by ANOVA". We find that an uncritical ANOVA by itself rarely relates to the experimental objectives.

There are many reasons why researchers need to reconsider their approach to data analysis. One reason is that more research in the developing world is being carried out on-farm, where the simple and traditional experimental designs are often inappropriate. Data are often codes, perhaps on a 5-point scale, as well as continuous measurements, such as crop or milk yield, and many different variables are collected. The data often have greater complexity than on-station trials, with information being recorded about the farmer - e.g. farmer practice, size of farm etc. - as well as being collected at the plot level, such as crop yield.

This guide offers guidance to researchers on a reliable approach to the analysis of on-station and on-farm trials. The analysis should satisfy the objectives of the experiment and ensure that the researcher gets as much as possible out of the data collected. This approach is described in Part A of this guide. Part B summarises some common complications that often arise in the analysis of experimental data.

Part A: Strategy for Data Analysis	Part B: Complications in experiments
A1. Introduction	B1. Introduction
A2. Objectives of the Analysis	B2. Multiple levels
A3. Understanding Variability	B3. Repeated Measures made Easy
A4. Preliminary Analysis	B4. Surprise Complications
A5. The Role of Analysis of Variance	B5. Finally
A6. Statistical Models
A7. Have I done my analysis correctly?

Part A: Strategy for Data Analysis

A1. Introduction

A2. Objectives of the Analysis

The first stage is to clarify the objectives of the analysis. These are based on the objectives of the study and therefore require the experimental protocol. It is important to link design and analysis at the planning stage of a study, since the objectives of an experiment should be given in the protocol in such a way that they define the treatments to be used and the measurements that are needed.

Some experiments have just a single treatment factor, such as ten varieties of maize, plus one or two control treatments representing the varieties in current use. An objective might then be to decide whether to recommend some of the new varieties, compared to the ones currently in use. This recommendation could be based on one or more criteria such as high yield, or acceptable taste and these correspond to the measurements taken.

Many trials have a factorial treatment structure, with two or more factors, such as variety, level of fertiliser and frequency of weeding. In such trials there are usually more objectives - some that relate separately to the individual factors and some to the more complicated recommendations that would be needed if the factors do not act independently of one another. Where treatment factors are quantitative, such as amount of fertiliser, the objectives are often to recommend a level that produces an economic increase in the yield, compared to the cost.

The above examples emphasise the key role played by the objectives of the trial in determining the analysis. In principle the objectives in the protocol and the objectives of the analysis will be the same, but the objectives of the analysis may be different for a number of reasons.

* The objectives of the study may have been stated in a vague way

* There may be other, unstated objectives that may be added, given the data that are available

* Some of the original objectives may not be possible, either because the required data were not measured or because of unexpected complications during the trial.

The objectives of the analysis may evolve as the analysis progresses.

In realising the objectives, it is often necessary to clarify the response variables of interest. For instance, if the objective of the trial is to look at the disease resistance of a crop, and individual plants in a plot are assessed on a scale from 0 (no disease) to 5 (very badly diseased), how is disease resistance to be assessed? Is it, for instance, by the proportion of plants in a plot that are disease free? or by the mean or the maximum disease score of the plot? Normally, the variables proposed are specifed in the experimental protocol.

We strongly recommend that this preparatory stage include the preparation of the initial dummy tables and graphs that the scientist feels will meet the objectives of the analysis. They will usually use the treatment means, because the treatments were chosen to satisfy the objectives. The specification of these tables and graphs should define the particular measurements that will be used.

Thus, in the first example above, where new varieties of maize were being compared with ones in current use, our "dummy" table may look like:

Variety	Mean Yield (kg/ha)	Ranking of taste
Control variety 1	...	...
Control variety 2	...	...
Variety A	...	...
Variety B	...	...
etc, in decreasing order of mean yield.

In the second example, a graph of mean "profit" (i.e. yield - cost of fertiliser) on the y-axis, versus amount of fertiliser on the x-axis, might be suggested as one presentation.

A3. Understanding Variability

The variability observed in data from plots or animals in an experiment can be due to the treatments which were applied, to the layout (e.g. in which block the plot is sited - a shady area as opposed to sunny site), and to the fact that any two plots experiencing the same experimental conditions give different yields - i.e. the plot-to-plot variability. The analysis is concerned with explaining the variability in the data, and determining whether, for instance, treatment effects are larger than would be expected of random variability.

Most statistical textbooks describe data analysis in terms of mathematical models and Greek letters such as and . Here we prefer a more practical approach and use the following general form to describe the data for any particular measurement in an experiment:

data = pattern + residual

Pattern is the result of factors, such as the experimental treatments and other characteristics often determined by the layout.

Residual is the remaining unexplained variation, which we will also seek to explain further (Section 7).

Identifying that part of the pattern that is due to the treatments is an important part of the analysis, because this relates directly to the objectives of the study.

All data analyses depend on this framework, and we return to it later when discussing more formal methods of analysis. The type of measurement also determines the analysis method, and data such as yields, fall within the class of "Analysis of Variance" or "Linear Models". Other types of data, such as insect counts, number of diseased leaves per plant, or preference scores use "Analysis of Deviance" or "Generalised Linear Models" - but the idea of expressing variability in terms of pattern and residual still apply.

A4. Preliminary Analysis

The simple methods described here apply similarly to all types of data. Assuming some tables and graphs have already been identified from the objectives, it is easy to "fill in the numbers" and observe the patterns of response. This is the use of descriptive statistics to explore the patterns of interest, such as the treatment effects.

Boxplots, scatter plots and trellis plots are all useful tools of exploratory or initial methods of data analysis (sometimes called EDA, or IDA). They give insights into the variability of the data about the treatment pattern and highlight any outliers that need further clarification. Suspected patterns, such as block effects or a fertility gradient can also be explored, and sometimes unexpected patterns emerge that the researcher may want to investigate further.

The graph below shows a simple example of an exploratory analysis, where the main objective of the trial was to suggest the high yielding varieties. It shows that the yields in all three replicates are consistent except for Variety 7, which has yields of 2.4, 2.0 and 1.4 tonnes/ha in the three replicates. Clearly something is odd! Examination of other variables confirmed that the problem was not a typing error, but it was too late to return to the field. One possibility is to omit Variety 7 from the formal analysis and report its results separately.

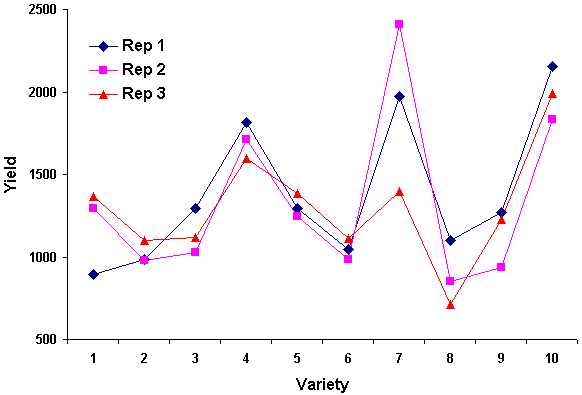In simple experiments these preliminary phases may take just a short time. In contrast, in a large on-farm study, most of the analysis consists of (a) summarising the interview data as simple tables and (b) looking at treatment comparisons in subgroups of farms. The preliminary work therefore constitutes the bulk of the analysis, and is crucial so that the researcher can recognise the patterns in the data.

Once the appropriate descriptive statistics have been tabulated and/or graphed, the researchers has been able to draw some, albeit subjective, conclusions about the study objectives. It is therefore possible to write a draft report of the study!

We are advocating here that a researcher can learn a lot about the data by paying close attention to the objectives and producing some summary tables and graphs. So why not stop here? What is the use of ANOVA and of more formal methods of analysis?

There are two main limitations to the exploratory analysis. One is that the data can only be looked at in "slices". For example we can look at the pattern due to treatment (and the residual variability) ignoring blocks, and then look at the pattern due to blocks; but it is difficult to look at several components of the pattern at the same time. This is particularly important when there are many factors or when data structures are complicated as in large on-farm trials. We need a method of apportioning variability across different sources all at once and this is the role of ANOVA.

Second, the conclusions drawn from the summary tables are still subjective. Some measure of precision needs to be attached to the effects observed. For this we need more formal methods of analysis.

A5. The Role of Analysis of Variance

5.1 As a descriptive tool

5.2 Exploring the treatment structure further

5.3 Statistical Inference

Most scientists know that ANOVA is the key tool in the analysis of experimental data, yet many do not know how to fully interpret it. Here we illustrate what it provides in addition to the tables of means that have been used above.

5.1 As A Descriptive Tool

In the previous section we introduced the idea that, for any measurement, we can consider

data = pattern + residual

as a summary of the variation in our data. The analysis of variance is a technique with which we can look at the whole pattern, e.g. blocks and all treatment factors together, and identify the components that are important. Also, because it extracts all the pattern, it also provides an opportunity to look at the residuals, i.e. the part of the data that can not be explained by the model, or pattern, in the experiment.

The ANOVA table contains elements called sums of square, degrees of freedom and mean squares for both the components of the pattern and the residual.

Source	d.f.	SS	MS
Pattern For example: Blocks Treatments	... ...	... ...	... ...
Residual	...	...	...
Total	...	...	...

The sums of squares allow us to see what proportion of the variation is explained by the different parts of the pattern in the data. The residual sum of squares shows us what remains unexplained, whilst the residual mean square, which estimates the variance of the units ,should be as small as possible so that differences between the treatments can easily be detected.

Each observation has a contribution to make to the residual sum of squares, and one large aberrant observation can have a large impact on this. These individual residuals should therefore be inspected for their influence on the estimate of random variability. Most statistical packages will automatically indicate which observations have large residuals, and these should warrant further investigation. Thus the first use of ANOVA is as an exploratory tool.

In trials where there is more than one treatment factor each line in the ANOVA table corresponds to a table of treatment means. Thus the ANOVA table can be used as a sort of "passport" to the respective tables of means. This can help us decide which tables to use to present the results. For example, in a 2-factor experiment, with variety and fertilizer we may have proposed to present the means for each factor separately. The ANOVA table may indicate that a large part of the pattern in the data is due to the interaction between variety and fertiliser, thus suggesting that we should instead present the 2-way table of means.

5.2 Exploring the treatment structure further

We now return to the objectives of the trial. The next step in the analysis of variance is to identify which parts of the (treatment) pattern relate to the different objectives and then to examine the corresponding sum of squares and effects. For qualitative treatment factors, (like variety) this is often through the use of treatment contrasts. For quantitative factors, like the spacing factor above it is often through a consideration of the line or curve that models the effect of the changing level of the factor. These graphs have normally been given earlier, see Section 3, but we now know that they arise from a treatment effect that has explained a reasonable proportion of the variability in the trial.

5.3 Statistical Inference

In the previous section we have discussed the ANOVA table without the distraction of F probabilities and t-values - we now add the ideas of statistical inference. The concepts are reviewed in the guide on statistical inference and this guide assumes the basic concepts. These include the ideas that the standard error of an estimate is a measure of its precision, and that a confidence interval for a treatment mean is an interval likely to contain the mean and not an interval that contains most of the measurements for that treatment.

The first part of statistical inference in the analysis of experimental data is usually the F-probabilities that are given in the final column of the ANOVA table above. They enable us to test certain hypotheses about the components of the pattern part of the data. The p-values (significance levels) and the magnitude of the relevant mean squares in the table are the "passport" to help decide which components of the pattern we wish to look at in more detail.

This "passport" must not be used too strictly! The significance test is usually one of no treatment difference, between any of the levels, which is almost certainly untrue. What we usually want to find out is whether any of the differences that relate to the objectives can be estimated with any reliability, given the "noise", i.e. the residual variability that is in the data.

The second main component of statistical inference is the standard errors that are associated with the important differences in treatment effects. We recommend that tables of treatment means be accompanied by the standard error of a difference, rather than the standard error of treatment means, since it is usually the difference between treatments which is of interest in a trial. Values for any important treatment contrasts should be accompanied by their standard errors and normally reported in the text. The guide on presentation also gives some guidance on the presentation of graphs.

For simple experiments we do now have all the tools that are required to conduct a full analysis of the data and write a report.

A6. Statistical Models

We include the subject of statistical models in this guide for three reasons. The first is that an understanding of these models enables a wide range of experiments to be analysed quite easily. The second is that a description of the statistical model provides an easy way to explain the assumptions of the analyses. The third reason is that once the researcher understand the principles of modelling, he can extend these ideas to other types of data.

The essentials of the model have been given already i.e.

data = pattern + residual

We now formalise this description by defining specific examples. One is of simple regression, where yields may be related to the quantity of Nitrogen in the soil by

Yield = a + b.Nitrogen + residual

if there is a linear relationship between Yield and Nitrogen.

This is an example where the pattern in the yield is a result of its relationship with a variate, but the idea is the same if we include factors in the model. So in a simple randomised complete block trial of varieties, we might consider the model as:

Yield = Constant + block effect + variety effect + residual

A third possibility is that we have a mixture of both variates and factors in the model, for example

Yield = a + b.Nitrogen + block + treatment + residual

One more bit of terminology is that the idea now is to estimate the unknown "parameters" in the model, for example the slope of the regression line would be a parameter in a simple regression model. In the models with factors, the estimates of the treatment effects are particularly important, because they relate to the objectives of the trial.

Once users are familiar with the idea of simple linear regression, these models with factors are all simple to fit, with current statistics software. Most packages by have an "ANOVA" facility for the analysis of data from simple experiments and a regression facility for this more general approach.

What does the user gain and lose by this new modelling approach, compared to thinking in terms of the treatment means as a summary of the effect of each treatment? If an experiment is simple, such as a simple randomised block design, then the modelling approach is identical to using the simple approach. Thus the estimates of the treatment effects are simply the treatment means. In such cases the ANOVA facility for the analysis usually provides a clearer display of the results than the use of the regression approach and is usually used.

The modelling approach comes into its own when the experiment is "unbalanced", or there are several missing values. For example, in a simple on-farm trial all farmers may have the same three treatments and so each farmer constitutes a "replicate". In a more general case, perhaps one or two treatments are in common and farmers then choose other varieties they would like to try, on an individual basis. There may be a total of eight varieties overall and an initial examination of the data indicates that the model for the yields of

Yield = Constant + Farmer effect + Variety effect + residual

is sensible to try. This now needs the more general approach and the estimates of the variety effects would not necessarily be the simple treatment means, but would automatically be "adjusted means", where the adjustments are for the farmer differences. It should be clear that an adjustment may be needed to compensate for the possibility that a particular variety might have just been used by the farmers who tended to get better yields. As some treatments were in common for all farmers, those yields provide information to make the adjustment.

Note: There is some confusion in terminology between the term ANOVA as used to denote the analysis of a simple experiment, and the ANOVA table which is given by both approaches as an initial summary of the data.

A7. Have I done my analysis correctly?

We suggest that thinking in terms of the modelling approach is also useful to examine both the assumptions of the proposed model and whether it can be improved. In examining a model, we examine its two parts. First are we happy with the "pattern" component" and second, with the "residuals"?

We often look at the residuals to check if they still contain some extra part that we could move into the pattern. In the example above, the model assumes that a good variety is good for all farmers. Perhaps there is an excellent variety for farmers who don't have striga on their plots, but with striga present it is not so good. If we have also measured striga incidence on the plots, perhaps just as present or absent, then we could add it to the model. Or, if there were just a few farmers with striga, we could simply split the data and look separately at the non-striga farms.

It is also important to check the residuals in a model to see if they satisfy the assumptions of the analysis. One assumption is that the residuals are from a normal distribution. This is not usually critical, but it often helps to check if there are odd observations that need special examination. A second, and more important assumption is whether the data are equally variable, because the ANOVA and regression approaches both assume there is only one measure of spread for the whole experiment. With variables like yields, splitting the data into subsets is an effective of dealing with this. Alternatively, in some circumstances, it may be more sensible to transform the data.

---

Part B: Complications in experiments

B1. Introduction

Researchers sometimes state that they "only do simple trials", as a reason why their pre-computer training in statistics is sufficient, but in our experience it is rare to encounter a trial that does not have some unforeseen complication. Indeed, perhaps a trial with absolutely no complications is "too good to be true!"

The three main components of a trail ate the treatments that are applied, the layout of the experiment and the measurements that are taken. Describing which of these components has become more complicated is useful in categorising the types of solution.

One of the most common complications in experimental data arises because aspects of the trial are at multiple levels. For example in an on-farm trial there are normally some measurements at the farm level from interviews and at the plot level from yields. A related problem that is common in many trials and that is of repeated measurements, as in the case of milk yields or weight gain measured on the same animals on several occasions over a period of time. Both of these complications are to some extent planned, as they are part of the design of the experiment, but there are also unexpected complications that can arise. Here we discuss multiple levels and repeated measurements, and then give some guidance on some of the common "surprise" complications.

B2. Multiple levels

2.1 Introduction

2.2 Dealing with multiple levels

2.1 Introduction

In a simple randomised complete block experiment, with treatments applied to the plots and a single measurement (e.g. maize yield) made on each plot, the analysis is simple. Treatments and measurements are at the plot level - and so the treatment effects are assessed relative to the variation between plots.

In many experiments, though, the experimental material have a multi-level structure. To explain this, consider the situation where the experimental unit, to which treatments are applied, is a plot containing a number of trees for crop experiments, or a pen containing a number of animals for livestock trials. If measurements are taken for individual trees within each plot, or animals within each pen, then the data have been collected at a lower level to that of the treatments.

Such experiments are sometimes wrongly analysed, because the different levels of the data are ignored, thus giving the impression that there is much more information than there really is. Failure to recognise the multi-level structure mixes up the between and within pen (or plot) variation. This can result in wrong conclusions being made about the treatments, since the within pen variation is often much less than between pen variation.

A split plot experiment is a common example where the treatment factors are applied at two levels, i.e. some to the main-plots and others to the sub-plots. In this case data are usually collected at the lowest level (e.g. subplots). Although this is a common experimental design the complication is that the analysis still requires the two different levels of variation to be correctly recognised. Many common statistics packages produce the correct analysis of variance table, but do a poor job in presenting the full results for this design. Very few supply all the standard errors needed to compare the different treatment means.

A third example of multiple levels is a lattice design - used for large variety trials, where there are more treatments than can be accommodated in a complete block design. Here the multiple levels are in the layout component. Thus the treatments and measurements are all at the plot level, but the layout consists of replicates and then blocks within the replicates and plots within the plots. Again, these multiple levels must be recognised in the analysis.

Many on-farm trials combine characteristics of a survey and an experiment, and they too have a similar hierarchy to the examples above. For instance the layout structure might have many levels, perhaps village, then farming group within village, then household, then the field, and finally the plot within the field.

In on-farm trials each farmer is often the equivalent of a "block" or "replicate". The treatments are applied to plots within the farm and some measurements are taken at the plot level. However, we also interview the farmer, or observe characteristics of the whole field, thus we take these measurements at the farm level which is higher than that at which the treatments were applied. Some measurements, as in a participative study, could be from a higher level still, perhaps from discussions at the farming-group level.

2.2 Dealing with multiple levels

Once the correct multiple levels structure is recognised in data, some of the analysis complications can be overcome. There are two obvious strategies, which we consider in turn:

* eliminate the different levels and conduct each analysis at a single level,

* accept the different levels and analyse the data as they stand - as in a split-plot analysis.

Trials where soil measurements are made within each plot are an example where the data are collected at a lower level to that at which the treatments were applied. For example 5 cores may be made within each plot, but then be reduced to the plot level, by mixing the soil before analysis. This is the same idea as scoring 10 plants for disease within each plot, and then calculating a summary statistic, such as the mean disease score, before the main analysis.

We suggest that this is the appropriate solution for many studies where measurements have been taken within the plot. The summary is now at the plot level, where the treatments were applied and the analysis proceeds. When the data are individual measurements of height, weight or yield, then usually a mean or total value for the plot is all that is required.

Sometimes, depending on the objectives, more than one summary value will be calculated. For instance, disease severity might be assessed in terms of the mean disease score, the number of plants with a disease score more than 3, and the score of the most diseased plant.

In general we recommend that the raw data at the within plot level should be recorded and computerised, rather than only the summaries at the plot level. This is partly for checking purposes and also for ease of calculation. The computer is a tool to assist the researcher in the analysis, and should be used for as much data management and calculation as possible.

On-farm trials often have measurements at the plot level - where the treatments were applied - and the farmer level, with data from interviews. Plot yields are used for the objectives related to the observed performance of the treatments, and the interview measurements relate to objectives concerned with the farmers priorities and views. Here there is no problem: we analyse each set of measurements at its own level.

The difficulty in analysing on-farm trials arises, because we often need to combine information across the two levels. For example there may be large variability in the effect of the treatments (plot level), and we believe some of this variability could be explained by the different planting dates, recorded at farm level. The solution is easy where there are just two treatments. Then we just calculate the treatment difference for each farmer, which is a single value, and relate it to the other farm-level data.

This solution can be extended to situations where there are more than two treatments per farm, by applying the same approach to the important treatment contrasts in turn (see Section 5), and relating them to the other farm-level measurements. However, this is a "piecemeal" solution and not particularly suitable if there are more than four treatments, or the treatments have a factorial structure. The alternative is to use a multi-level, or mixed model, analysis which can handle the data over the two levels. This approach is similar to a split-plot analysis - main plots are the farms - except that the data are unbalanced. It is discussed briefly in the final section of the guide.

B3. Repeated Measures made Easy

Many experiments include the "problem" of repeated measurements, either in time or in space. In an animal experiment we may record the weight of the animal each month. We may harvest the fruit from trees each season, or record the disease score each week and so on.

These are situations where the treatments are applied at the plot or animal level and measurements are then made at a lower level, i.e. at time points within each plot or animal. It is tempting to think of this as a multiple-levels problem and we do not resist this temptation. Indeed we claim here that the same "solution" is usually possible as was described in the previous section for the case of measurements taken on plants within plots.

The important difference between the 10 plants per plot and the "repeated measures problem" is that the 10 plants are normally selected at random. If instead they are deliberately taken along a diameter, and their position noted, then they become a repeated measure in space.

Thus the new feature is that these measures are "in order" and it is usually important to take account of this part of the structure in the analysis. In terms of preliminary analysis the first step is usually to graph the raw data, i.e. to produce a time-series graph showing the development of the measurement for each experimental plot or animal. For simple summaries of the experimental treatments the graphs are often conveniently grouped so that all the lines corresponding to the same treatment are on the same graph. An example is shown below.

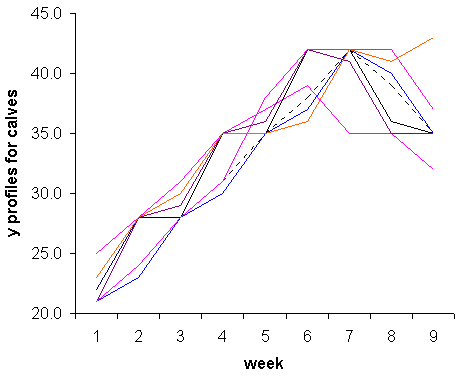This figure depicts milk consumption over an eight week period for individual calves all being fed the same food supplement. It shows that milk consumption increases in a fairly linear fashion over time until about weeks six or seven, after which time it starts to level off or decrease. We can also see that consumption becomes slightly more variable at the later times.

Such graphs, together with the objectives of the trial, will normally indicate the summaries that should be taken of the repeated measures, at the unit (animal or plot) level. Thus, as in the previous section, we eliminate the problem by moving the repeated measures data up to the level of the experimental unit. The reason this is usually sufficient is that the objectives are usually directly related to the different treatments and they are applied at this higher level.

As with the multiple levels situation, there is no one "standard" summary with repeated measurements. It may be the value measured at a particular time point, or the difference between the value at two points, or something more complicated. For instance, had our example above related to liveweight gain animals, then a reasonable summary might have been the slope of the regression line over the first six weeks of the study.

More "advanced " procedures are available for the analysis of repeated measures data, which extract more information from the data. These are not discussed here, because we feel that for most situations the simple approach outlined above is sufficient.

B4. Surprise Complications

The table opposite lists some common complications which can arise in experimental research. They are categorised as complications relating to the treatment structure, the layout or the measurements. For example, farmers may not apply exactly the treatments specified, there may be missing plots, or there may be some zero or otherwise odd values.

Type	Complication	Example
Treatment	Levels modified	Farmers applied "about" 100kgs of mulch
	Applied to different units	Seed shortage of one variety, so control applied to multiple plots in reps 3 and 4.
Layout	Post-hoc blocking useful	Observations indicated that blocking should have been in other direction
	Missing values	a) Some farmers left trial. b) Some yields missing on 3 out of 36 plots. c) Some plants missing within the row.
Measurement	Zero values	Some trees did not survive
	Strange values	Yields for one farmer had different pattern to the others
	Censored values	All trees counted, circumference only measured on large trees
	Different variability	Soil nitrogen values showed more plant to plant variation in some treatments
	Affect treatments	a) Some plants heavily affected with striga. b) Some farmers have streak virus.

We describe six alternative strategies for coping with such complications.

• The first is simply to ignore the problem: this is sometimes the correct strategy. For example in a study on leucaena where an objective was to estimate the volume of wood, all trees were counted, but the circumference was not recorded on the small trees. This could perhaps be ignored, because the small trees contribute little to the volume. Alternatively our second strategy is to modify the objectives, or the definition of a treatment or measurement. With the same example, we could modify our objective to one of estimating the volume of wood from trees with a diameter of more than 10mm.
  
  
• Sometimes the complication means that an objective has to be abandoned. This does not imply that the analysis need be abandoned, because other objectives may still be obtainable. In some cases the problem can be turned to your advantage in that new objectives can be studied. For example, in an on-farm study, two of the treatments involved the farmers applying 100kg mulch. In the actual trial the quantity applied varied between 11kgs and 211kgs. This might permit a study to be made of the effects of applying different quantities of mulch. However we find that such complications are usually more useful in re-assessing the design of the subsequent trial. Here we encourage scientists to be flexible in their approach. Thus in the redesign, not "How do we force the force the farmers to apply 100kgs?", but "I wonder why the quantities they applied was SO variable?"
  
  
• The third strategy is a "quick fix". With missing values a common quick fix is to use the built-in facilities in many statistics packages, namely to estimate them from the remaining data and then proceed roughly as if the experiment did not have the problem. A quick fix in the problem of the small stems in the leucaena trial, mentioned earlier, might be to assume they are all 5mm in diameter.
  
  
• Quick-fixes are not risk-free even if they are built into a statistics package and we caution against using the automatic facilities for estimating missing values if more than a tiny fraction are missing. It is quite easy to use our fourth strategy, at least to check that the approximate analysis is reasonable. This is to use a more flexible approach to the modelling. That often means we move from the ANOVA to the regression approach, because the latter does not need balance. Hence it can adjust for missing values properly. Similarly the regression approach can be used in a trial where post-hoc blocking would be useful, because the initial blocking was the in the wrong direction.
  
  Sometimes the more flexible approach implies that a transformation of the data would give a more reasonable model. Alternatively where some treatments are more variable than others, the solution is to analyse the data separately for the two groups of treatments.
  
  
• The fifth approach is to do a sensitivity analysis. For example, with transformations or odd observations, for which there is no obvious explanation, it is usually very quick to do two or three alternative analyses. These correspond to different models. If there is no difference in the conclusions then the results are not sensitive to the particular model. It is then often useful to report your investigation and then use the model that is simplest to interpret in relation to the objectives. Where the conclusions do change you know that more work is needed to identify the appropriate model.
  
  
• The final strategy is to build a model to try to solve the problem. For example, with the leucaena stems it might be possible to build a "one off" model for stem diameters of leucaena trees. Often the construction of this model was not part of the original objectives and may not be needed - the quick fix is sufficient. But it may be interesting and of general use later. Thus it adds a methodological objective that is of general use and may be incorporated in the design of a subsequent study.

B5. Finally

In this guide we have tried to give the impression that the analysis is driven by a sense of curiosity about the data and flexibility in the approach. The key is simply that the analysis should relate directly to the objectives, so they are satisfied as far as is possible given the data.

We have also attempted to give guidance on how to deal with some complications which arise in data analysis, which could be dealt with using sophisticated methods, but where often a simple solution is all that is necessary. We have not attempted to discuss complications where more advanced approaches are often necessary. However there are two instances where such methods will often be required and we briefly mention them here.

The first concerns the type of data and the second returns to the issue of multiple levels. Trials typically include measurements of different types. There are measurements on yield. There may be counts of weeds per plot, a disease score may be on a scale of 1 to 9 per plot, each plant may be recorded as germinating or not, etc.

Any of these types of measurements may be summarised with the simple methods described in the preliminary analysis, but instead of summary tables of mean yields, we now use tables and graphs of counts or percentages, e.g. of farmers who valued a particular variety.

The standard ANOVA and the regression modelling assume the data are from a normal distribution, and are no longer directly applicable for these types of data. Hence researchers often transform the data to make the assumption of normality more reasonable. However, there is a more modern alternative approach. The simple modelling ideas described in section A6 are often called "general linear modelling" and the "general" implies that it applies to balanced and unbalanced data. The analyses can be extended to "generalised linear modelling" where the "generalised" is because it applies to other distributions besides the normal.

The second main area which requires more complex methods is where the data are at multiple levels and the simple approaches are not sufficient. Multiple levels cannot be handled by the modelling approach described earlier, because this is limited to information at a single level.

The standard ANOVA will handle multiple levels, only for balanced data, as in the case of the split-plot trial. So, just as the regression modelling approach generalises the single level ANOVA, we need an equivalent to the split-plot analysis to generalise to situations where data are unbalanced.

An example of this is the on-farm trial described earlier where we now want to relate some of the farm-level measurements, such as striga infestation, to the plot-level yields, but there are unequal numbers of farms with and without striga, and not all farmers grew the same three varieties. We want to study the interaction table in the same way as we would in a standard split plot analysis, with one factor (striga) on the main plots and the other (variety) on the subplots, but the data structure is unbalanced.

Multiple levels can not be handled by the modelling approach described in Part A, but need their own type of modelling. This is called mixed-models or multi-level modelling, and is sometimes known by the names used by statistical software, such as REML in Genstat or PROC MIXED in SAS.

Both the topics of non-normal data and multi-level modelling form the material of a further guide.

Last updated 11/04/03

© 2005 Statistical Services Centre ~ The University of Reading | Terms & Privacy | Feedback