Some Basic Ideas of Sampling
Release date: November 2000
This is one of a series of guides for research and support staff involved in natural resources projects. The subject-matter here is sampling. Other guides give information on allied topics. Your comments on any aspect of the guides would be welcomed.
1. Introduction
2. Study Objectives
3. Units
4. Comparative Sampling
5. Representative Sampling - general ideas
6. Doing one's best with small samples
1. Introduction
1.1 Who is the booklet for?
There are a few comments on sampling in our earlier booklet Guidelines for Planning Effective Surveys, but the broad ideas on sampling, presented here, are much more widely relevant - they are a form of general knowledge - and have something to offer to qualitative and quantitative studies alike. The illustrations and examples are concerned with international development work in the natural resources field, and the content is meant to be accessible to project staff in this area, and to those who review project activities. Field research projects inevitably concentrate scarce resources on a small "sample" of units, such as forest, or peri-urban, areas, and the people in them: the challenge is to do so while still producing widely useful results.
We talk mainly in terms of human informants, rather than insensate units. We make a few comments about the sampling of activities, terrains, crops and so on which may arise in looking at respondents' environments and livelihoods. We do not attempt to cover the special needs of e.g. soil scientists or ecologists in whose studies there may be a much greater emphasis on topics such as systematic sampling, i.e. points evenly-spread in space or time.
1.2 What is the booklet about?
Subject-specific adaptations and extensions of the key sampling ideas exist in specialised literature for many fields of application. Unfortunately, general textbooks on "statistical" sampling often obscure the ideas by concentrating on difficult formulae for limited purposes, and more accessible presentations are frequently shallow, sectoral or polemical.
This booklet is about ideas needed to devise an intelligent sampling plan, and is not a cookbook. We are concerned with basic, widely useful ideas. Our aim is to present general principles for achieving good, defensible sampling practice, by the systematic application of common sense rather than mathematics. When committing resources, sampling is often a crucial stage. Checking with an understanding statistician can often improve efficiency and effectiveness at this point; the booklet defines what a statistician would like you to think about before such a consultation.
Section 2 looks at the definition of objectives. Our experience is that the objectives of sampling can be hard to pin down; they may not be expressed explicitly enough to fit with the imperatives of operational decision-making. Section 3 looks at "units". Except in rather trivial cases, there are usually several types of unit e.g. individuals, households or areas of land. Each will be the focus of some part of the study analysis and reporting, but confusion is common. One reason is that the same informant may be representing herself as individual, her household, the land she farms or other entities. Section 4 moves to slightly more specialised issues where the aim is primarily to compare, and to look at what differentiates, subgroups in the population.
Much sampling with human respondents is constrained by their willingness to cooperate. We then need to think carefully what results represent, and section 5 looks at this issue. We often have to sample a very small number of units, when the reality we are looking at is very complex. If a small study is worth doing at all, how can we make the procedure as sound as possible? Section 6 comments on this knotty topic. Section 7 concludes the booklet by explaining why a cookbook could not be provided.
1.3 Simple random sampling and objectivity - a basic idea
The first sampling paradigm in quantitative research methods or statistics classes oriented to human subjects is commonly that of simple random sampling. In this case, there is an accessible, enumerated list of members of the population, they have no distinguishing features, and each has an equal chance of inclusion in the sample. That is natural enough - there is no reason to do anything else! It is often assumed that there is only one clear-cut objective in such idealised sampling, to produce a confidence interval for "the" mean of "the" measurement plus perhaps a sample size calculation. How different it all seems when selecting informants and sites in real research!
Simple random sampling is very seldom applied in practice, but the statistical theory at least provides some "feel" for the benefits of other schemes. As a broad generalisation, a stratified sampling scheme will provide improved estimates, but increased complexity and cost, while hierarchical (cluster or multistage) sampling will usually prove cheaper and easier to manage, though estimates will be less precise for a fixed number of subjects.
The main argument for "simple random sampling" is not that each member of a population has exactly equal chance of selection, but that sample membership is determined in an objective way, not influenced by personal preferences. In practice, there are various problems if we have a non-random sample; selection bias - conscious or otherwise - is important among these.
Probability sampling is the general term for methods where sample selection is objectively-based on known chances of inclusion in the sample. If the probabilities are known and non-zero, they don't have to be equal: corrections can be made to quantitative summaries. In difficult development project settings, inadequate time frames and sample frames i.e. listings from which to sample, incomplete respondent compliance etc. make it hard to ascertain probabilities. If these are unknown, but probably grossly unequal, it is hard to say what the results might represent. Even if it can't be done very well, it is good practice to be as objective as possible about sample selection, to equalise as far as possible the a priori chances that individuals are included in the sample, and to record procedures that support the claim to representativeness.
Random sampling offers the benefit that common, but unsuspected, peculiarities in the population will be "averaged out" in a large sample. If 30% of households are female headed, a random sample of 100 households should have not too far off 30% female headed even if we have not controlled for this. We could do so by taking fixed size samples separately from the male and female headed subgroups of the population i.e. stratifying by sex. Rarer features need larger random samples if their representation in the sample is to "settle down" to the right proportion. If samples are necessarily small, a greater degree of control may be needed to ensure the sample selected is not obviously odd. See section 6.
1.4 Hierarchical or multi-stage sampling - a central idea
Often "real-life" sampling involves hierarchical structures and sampling processes e.g. selecting countries where there are major issues about water rights, identifying and sampling localities where the issues are important, defining the groups with interests in the issues, then working out various suitable ways to sample and work with members of those groups. We refer to the largest units, countries in this case, as primary or first-stage units, the localities as secondary or second-stage, and so on.
In textbook terms, this is described as "multi-stage" sampling, the stages being the levels in the hierarchy - there is no implication of multiple points in time and unless otherwise stated, the sampling essentially gives a point-in-time snapshot. Frequently used, but all too often not fully understood, multi-stage sampling is stressed below.
A well-documented objective sampling procedure is particularly important where the units selected are "anonymous" i.e. the general reader of the research findings will not have detailed information about the individuals in the sample. In hierarchical sampling this applies least to primary units - maybe large "well-known" areas like provinces - and most to the ultimate sampling units - maybe households. As far as the latter are concerned, an eventual reader such as the person who financed the project, has no effective means of discerning how the sample was selected, and should be concerned about generalisability unless there is clear-cut reassurance that the sampling methodology was objectively based. Usually primary units are, perfectly reasonably, selected on a judgment basis; ultimate sampling units ought to be sampled in an objective way.
[TOP]
2. Study Objectives
2.1 Broad Objectives
2.2 More Detailed Objectives
2.3 Can objectives be met?
2.1 Broad Objectives
By broad objectives we mean a brief, general description of what it is hoped to learn from a study or a set of studies.
(i) One possible objective is to provide an overall picture of a population. For example if the national production of rice, plus stocks, will be insufficient to feed the people, rice will be imported: in such a case the objective is to come up with a reliable figure for the total size of the forthcoming harvest. The distribution of sampling effort in a crop-cutting survey must cover and represent the whole productive system.
(ii) A different type of objective is comparison. For example, an integrated pest management (IPM) strategy is to be tried in four Study Areas; the results are to be compared with a set of control areas. Here it is most important that the areas under the "new" and "normal" regimes are matched to ensure a fair comparison. Effective "coverage" of the population of land areas is less important than in (i).
Points such as the above are relevant when the overall picture or comparison is to be based on quantitative measurement and "statistical" analysis. We believe the same points apply equally forcefully even if more qualitative approaches to data collection are being used.
Note that (i) and (ii) above imply different approaches to sample selection and sample size. For the objective in the rice example (i) above, something close to proportional allocation of sampling effort is usually appropriate e.g. if one region produces about one quarter of the rice crop, it should provide the same proportion of the sample. Efforts should be made to correct in analysis for any disproportionate representation. This implies that producing an "overall" figure depends on having reasonably up-to-date and accurate information about relevant features of the population, i.e. a good approximation to a sampling frame. Carrying out one's own census-style enumeration exercise to produce a sampling frame is beyond the scope of most projects.
In contrast, in a case like the IPM intervention in (ii) above, the sampling frame requirement is generally much less rigorous as long as the main aim is a fair comparison. For instance, the example in (ii) above may invest half the field data collection effort in the Study Areas even if these represent a minute proportion of total planted area or production. At a later stage in the project cycle, this approach could change. After a "new" regime has shown economically important promise in some sub-areas, it may become worthwhile to delimit its range of beneficial applicability, i.e. "recommendation domain" and a reasonable sampling frame - a description of the whole population - is needed.
These two examples illustrate that if you ask statisticians to help produce an appropriate sample size or sampling pattern you should expect to be asked questions about objectives.
(iii) Sometimes the objective is to typify households, communities or other units to classify them into groups which may be studied, sampled or reported separately or which may become recommendation domains. This is like a mapping exercise where you have to work out where boundaries go: it usually involves a lot of observations. One problem case is where only a special group is covered, e.g. compliant farmers are recruited to a "panel" who will be visited for one or several studies in a project. Often the non-compliant are not studied at all, and this restricts the range of generality that can be claimed for conclusions. For example, readiness to adopt innovations may be higher for compliant farmers. At least we should know the proportion who are compliant, and have some idea how they compare to the others.
(iv) If a project encompasses a number of information-garnering studies in the same population, the objective may be based on a relatively long-term relationship with informants. It is often best to link up the samples across studies in an organised way to enable results to be aggregated and synthesised as effectively as possible. Say a (fictitious) three-year bilateral project identifies 150 farm households as possible collaborators, estimating that 50 may be lost to follow-up before the project ends. The anthropologist works in depth with seven households chosen on the basis of a baseline study of all 150 led by the economist. Their combined work leads to a division of the cooperating households into three groups with identifiable characteristics which might be tackled in distinct ways to achieve project goals. It is also useful to keep a simple population register for the 150 households, so that the selection of participants in follow-on studies takes proper account of their previous project involvements.
2.2 More Detailed Objectives
General notions of purpose, and broad descriptions of information to be acquired, are not sufficient to decide on sample size, or to provide assurance that results of a research study will be of the scope and type needed to progress. While detailed research results cannot be known in advance, it is essential to think, before committing resources, about what use will be made of the information.
The researcher should have a plan to use and report the findings and a plausible case that, barring the truly unforeseeable, the information collected will be necessary and sufficient for the purpose. Of course this case must show that other parts of the research strategy are under control as well as the sample selection! One of the inputs to sampling decisions is an understanding of the research instruments. Their qualities under the broad headings of "accuracy" and "stability" are important determinants of what should be sampled and how much.
Many studies have a plurality of general objectives, some of which may pull in different directions as far as sampling schemes are concerned. It is desirable to think out, record and refer back to the objectives and to check at each stage that the samples obtained are adequate to satisfy all important objectives. Done properly, this usually involves making the general objectives more specific in the course of e.g. prioritising them or compromising between their different fieldwork demands.
Note that a multi-stage sampling design, introduced because there is a hierarchy of units, will involve a need to define objectives at different levels of the hierarchy and priorities between them. It sometimes makes sense to sample within administrative units e.g. provinces, and use these as primary units. The objectives of a multi-stage sampling procedure have not been thought out properly unless this has been done.
Say the project output is an intervention package to be "applied" at village level. One "multi-stage" research strategy might focus on testing the package in two villages, collecting much detail about internal village organisation at household and individual level as it relates to the intervention package. At village level this is a sample of size two, and merely provides anecdotal or "case study" evidence that the effect of the package can be replicated elsewhere: too much of the information is at "within-village" level. An alternative strategy might treat one village as above, but divert the other half of the effort into briefer studies in five extra villages. There will be less information at the within-village level, but more knowledge at village level where it matters.
2.3 Can objectives be met?
Both the studies sketched in the preceding paragraph represent less bad, rather than acceptable, practice. Both are based on such small sample sizes that they should probably not be funded! Ideally, the specification of clear objectives should define the data and analyses expected and the worthwhile conclusions that can be anticipated, with a financially feasible and cost-effective set of activities to complete the work. The fact that intensive use of resources only permits a small study, e.g. a case study in one locality, does not prove that the very small study is capable of generalisation or of yielding conclusions that will be of real value in a wider context. All researchers need to face up to the possibility that a proposed study may be incapable of yielding results which are fit for the intended purpose, or even for a more modest and sensible purpose. There is much historic evidence that this issue has been ignored in the past in many fields of enquiry.
[TOP]
3. Units
3.1 Conceptualising the Unit
3.2 Unit levels
3.3 Profiling
3.4 Unequal Units
3.5 Qualifying units and population coverage
3.1 Conceptualising the Unit
Simple random sampling treats units as if they were like neon atoms, floating unreactive and to all appearances identical in a fluorescent tube. But human populations are socialised, reactive and interactive. Even with single respondents to a formal survey, the unit being researched and reported can be e.g. the individuals, their households, or their villages. Some units are easily defined, e.g. individuals. Households are more changeable through time. The multistage study involves different units at the different levels. Some may have a natural definition, others not, e.g. the farmer's maize field, and a plot within it where yield will be measured. There is a choice to be made in the latter case on how big a plot will give a sensible compromise between getting a good measurement and undertaking too much work.
3.2 Unit levels
Different "effects" come into play at each level of a hierarchical study e.g. the individual's educational standard, the intra-household distribution of food and the village's access to rural transport. If there are several levels in the study, much confusion stems from failure to recognise or deal with such structure.
Studies can become overly complicated and resource-hungry if they try to encompass many effects at many levels. Sampling can be conducted at several levels, and it is important to find an economical way of learning just enough about each level and its links to the others. One way to achieve this is often not to attempt to "balance" a hierarchical sampling scheme. The first strategy for the village-level intervention at the end of 2.2 suggested equally detailed studies in two villages. The alternative made the study into two different "modules", an in-depth study of one village and a broader study of several villages, perhaps using rather different methodologies. While the intention of the alternative strategy is to use the results of the two modules together, there may be no need to synthesise them formally if they address objectives at different levels.
3.3 Profiling
When consideration is given to how things evolve through time or space, an additional complication is overlaid on the study design. Regularly repeated observations can provide evidence of consistency or systematic change in time, especially if the same respondents are revisited each time; then the unit is a compound of person and times. Such sampling is often expensive compared to before/after studies. It cannot be avoided if the time track of events is intrinsic to the study, for example for seasonal calendars, or for a monitoring system which must capture and identify sudden changes in staple food prices; generally each time profile constitutes one unit e.g. one farm family's record of farming activities over one year is a unit.
In the same way, if a participatory activity involves a gathering of village women with a facilitator to thrash out a cause and effect diagram, the result is a single profile in the form of a diagram i.e. one "unit" - an unreplicated case study. If the focus is solely on that community it may be of no relevance to look at any other group's version of the diagram for the same issue. However, if the exercise is undertaken as research, any claim of generalisability will require more than one unit. A simple sample of units might involve several independent repeats of the same exercise in different villages. A more structured sample might compare the results from two or more facilitators working individually in matched samples of villages (pairs of similar villages): this may distinguish between the effects of (a) a facilitator's approach, and (b) variation between villages. With only one facilitator, (a) is being ignored. If the villages are not matched, it is hard to decide whether to attribute differences to facilitator or village; in statistical terms, the two effects are confounded.
3.4 Unequal Units
Often sampling is based on treating all units as equal in importance, but land holdings, enterprises and other sorts of unit may be of varied sizes and potentials. For summative (rather than comparative) purposes it may then be important to give larger units greater weight in sampling. Deciding on the appropriate measure of size is often a difficult issue with a variety of answers preferred for different issues within the same study, e.g. estates may be classified by number of employees, by planted area, or by production.
When a compromise size measure is used in sampling, varying weightings may be needed in analysis for different variables. With quantitative data there are clear-cut, if involved, ways to do this. As with other aspects of sampling, it is important that weighting systems are not under-conceptualised and are used effectively, e.g. with weights reflecting different sample sizes in villages, village population sizes, areas given over to commercial cabbage growing, or transport costs. Where weighting is used, statistical help may be needed to make the most of the data.
3.5 Qualifying units and population coverage
Recording of the sampling procedure includes giving a careful definition of the actual "population" sampled. Often field limitations cut down what can be covered, and therefore the domain to which the research can claim to be able to generalise. For example, when specifying a sample only certain individuals may "qualify" for membership, e.g. if compliance is a criterion. It is usually important to record the "hit rate", i.e. the proportion who qualify and are recruited out of those approached, and the types and importance of differences between those qualifying and those not. These provide evidence of what the qualifying sample truly represents.
Difficulties in accessing the target population are inevitable in many situations, and should not be glossed over as a source of embarrassment. A "research" sample is not worthless when it does not match the a priori population, but a clear description should be given of what the study has succeeded in representing. Often there are new insights worth reporting even tentatively, from the hit rates mentioned above or less formally from meetings, perhaps brief ones, with those who did not opt to comply.
The conclusions and associated recommendation domains resulting from research must be properly supported by evidence. It is a form of scientific fraud to imply without justification that results apply to the a priori target population which the researcher had ambitions to sample, if those actually sampled are a more restricted set which may differ in kind from the rest of the target population! For example, a sample might be restricted to farmers who are quickly and easily persuaded to try a farming system innovation. If these are compliant, higher-income, male-headed households, conclusions derived with them may not be applicable to low-income, vulnerable, female-headed households.
[TOP]
4. Comparative Sampling
4.1 Objectives
4.2 Stratification
4.3 Factorial structure
4.4 Putting small samples in context
4.1 Objectives
This procedure arises (i) where the study sets out to compare existing situations in areas that are clearly distinct, e.g. the incidence of damage due to a particular pest in high-grown as opposed to low-grown banana plantations, or (ii) where an intervention such as a pest management strategy is tried in one area and compared to a similar area without the intervention.
4.2 Stratification
The idea behind (i) is that of natural stratification. The population divides naturally into segments which differ from one another, but are internally relatively homogeneous, e.g. farmers, fishermen, and traders - here the stratification characteristic is occupation. Internal homogeneity, if it can be achieved, means that a relatively small sample will serve to typify a stratum reasonably clearly, so this can lead to efficient sampling. Stratification divides the population into a non-overlapping set of categories. These may be subdivided if we have a second stratifying characteristic, e.g. sex of household head.
4.3 Factorial structure
In a comparative study with several possible stratification variables, the objective may be to check which factors define the most important differences from one stratum to another. Say we considered communities which were near to/remote from a motorable road (factor 1), which farmed relatively flat/steeply sloping land (factor 2), and which had greater or lesser population pressures on land resources (factor 3). This produces 2x2x2 = 8 types.
For each factor, we are doing the absolute minimum to take its effect into account when we look at dichotomies such as flat vs. sloping. We are acknowledging that, because there are many complications in the real setting, we cannot investigate, describe, or come to conclusions about, them all. When taking such a sample, usually of few units, it is as well to include only cases that clearly belong to the categories and to exclude those which are marginal or doubtful for even one of the classification factors.
We might then select n communities of each of the 8 types, giving 8n sites to investigate. The number n should not be confused with the number of factors or the number of levels per factor. It is a separate, independent choice: if above it was feasible to look at 20 or so sites, we might take n = 3, so 8n = 24. If we then look at the differences between remote and accessible communities we have samples of 12 of each type, and these samples are comparable to each other, in terms of having the same mix of flat and hilly land, higher or lower population pressure. At the same time we have comparable samples of 12 flat land farmers and hilly land farmers, and so on. The "three studies for the price of one" benefit illustrated here applies whether we are conducting a formal survey, or a much more qualitative exercise with each community.
Note that the objective assumed here is to compare the levels of each factor, to decide which factors are important. We are not concerned that the 2x2x2 subgroups define equal sized subsets of the whole population, nor that population subsets are represented proportionately; probably not.
4.4 Putting small samples in context
The previous section assumes we are looking at a fair number of communities as primary units. What can we do if an in-depth investigation cannot be replicated that often? It still has to be conducted in a few communities selected from a complex range - 2x2x2 types in our crude example, but maybe only a handful can be looked at in depth.
As we argue with other small samples below, the in-depth study has more plausibility if it is positioned relative to a larger and more representative sample. So a relatively quick characterisation might be done in each of the 24 communities. Then an appropriate design for accompanying in-depth studies may be a systematically selected subset of the types of primary community.
The in-depth study might reasonably be based in four out of the 24 communities chosen from the eight combinations of near/remote, flat/sloping, and high/low population pressure as a "fractional factorial design": one choice is illustrated below so that each of the factors is included twice and appears once with each level of each other factor.
| Near Road | Remote from Road | |||
| Flat | Steeply sloping | Flat | Steeply sloping | |
| High Pop. | include | --- | --- | include |
| Low Pop. | --- | include | include | --- |
Note that the above ideas are concerned with one level of the multi-stage sampling process. They make no stipulation as to how sampling aspects of the study may be structured within communities, nor of course about other aspects of research methodology. The proper specification of a sampling plan often means producing descriptions of the research protocol for several different levels.
Comparative observational studies have important design elements in common with designed experiments, and the above illustrates one or two of the many design ideas that apply effectively to such sampling studies.
[TOP]
5. Representative Sampling - general ideas
5.1 Representing a population
5.2 Defining a sample size
5.3 Objective sampling?
5.4 Quota Sampling
5.5 Systematic sampling
5.1 Representing a population
Representing a population often entails dividing sampling effort according to the known importance or size of segments of the population, which thus entails relatively small samples from minor sub-sections of the population. Generally speaking, if you can predict that results will differ systematically from one stratum to another, it is desirable to ensure the strata are represented proportionately in the overall results, so as to give a fair picture. If particular sections of the population (say female-headed households or striga-infested fields) are important to the researchers, and may be reported separately, the population may be stratified on this basis (headship gender, or presence/absence of striga) and an interesting stratum sampled more intensely than others, provided its results are "scaled down" to the appropriate level in an overall summary.
5.2 Defining a sample size
There is no clear-cut sensible method of producing an answer to the question, "How big a sample do I need?" You have to think it through in the light of the objectives, the field data collection conditions, the planned analysis and its use, and the likely behaviour of the results. There are several situation-specific aspects to this; there is no universal answer.
Statistical
texts mainly discuss the case where the mean of a numerical observation
is estimated from a simple random sample. This can provide some
"feel" for other situations, as indicated in 1.3. The
essential component of formulae is  /
/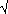 n,
n,
 representing
the standard deviation of the quantity sampled i.e. before you can
start working out a sample size to achieve a certain accuracy, you
have to estimate the variability you expect in your data.
representing
the standard deviation of the quantity sampled i.e. before you can
start working out a sample size to achieve a certain accuracy, you
have to estimate the variability you expect in your data.
More complicated cases are more common. Summaries from survey samples, for example, often take the form of tables, and the sample size required is then determined by the way responses spread themselves across the table cells, as well as the level of disaggregation required e.g. to three-way tables. As a simple quantitative example, if you can predict that you will need to look at tables of mean value of yield per hectare, for three types of land tenure, for five cropping systems, for male and female cultivators, you are dividing your data into 3x5x2 = 30 cells, and you need enough good data on areas, yields and their values to give reasonable estimates for all cells. If you decide that requires 7 responses per cell, then you have to target 7 x 30 = 210 adequate responses. This of course is a net figure and the planned sample size must be a grossed-up version which allows for those who are unavailable, unable or unwilling to participate. If that seems more than the budget will stand, think how the objectives can be made more modest: maybe you only need accurate figures for some of the totals, not for every individual cell.
5.3 Objective sampling?
Objectivity was singled out in 1.3 as the main reason for "random", or probability-based sampling. If the sample is selected on the basis of administrative convenience, personal preference, vaguely substantiated "expert" judgment, or its supposed evocative power, it is unavoidable that there will be the appearance or suspicion of bias - a serious failing in research. It is unfortunately rather hard to organise a probability sample without a good sampling frame.
Rather than trying to list the entire set of units, multi-stage samples can involve the development of just the essential elements of population listing. For example, at the first stage, we know the locations of districts and their administrative centres. When we select and visit some of these, we can ascertain the names of all the functioning government veterinarians in these districts. When we select and visit some of these, we can ascertain the names of all the villages they serve, and in turn of livestock owners in the villages.
5.4 Quota Sampling
Quota sampling is a method much used, for example by market researchers and others, to get round sample frame problems. It is not a random sampling method. It usually entails determining that the sample should be structured to control certain gross characteristics. A sample of 100 individuals might be required to be divided into three age ranges 15-39, 40-64, and 65+ with 20, 15 and 12 males, 20, 17, and 16 females, say to match a general population profile where women survive longer. The procedure does not require a detailed sample frame and is relatively easy to carry out as long as there are not too many tightly defined categories to find. If repeat rounds of independent surveying are done, e.g. monitoring public opinion without following up the same individuals each time, quota sampling is an easy way to ensure successive samples compare like with like.
Often the quota-filling task is left to interviewers' discretion with respect to accessibility, approachability and compliance as well as checking on qualifying characteristics, e.g. currently-married, main employment on farm. Insofar as it involves subjective sampling, the method is open to interviewer effects and abuses, which need to be controlled with care. The problems may be negligible if interviewing is relatively easy and well supervised: with small samples the subjective element of selection can be a serious worry.
5.5 Systematic sampling
This is a technical term implying samples are taken at regular intervals, down a list or in space or time. The frequency of sampling in time is a typical concern, and regularity is usually more desirable than arbitrary intervals. Sampling may need to be more intense in periods of particular activity e.g. to catch the peak prevalence of an epidemic. It certainly needs to be frequent enough that episodes of phenomena of major interest are not missed between sampling occasions.
[TOP]
6. Doing one's best with small samples
6.1 The problem
6.2 Putting small samples in context
6.3 Ranked set sampling
6.4 Sub-sampling
6.5 Post hoc validation
6.6 The £2 coin
6.1 The problem
The above approaches are reasonable when there is an adequate sample size, but what do we do when a very small sample is unavoidable? Say the researcher wishes to involve herself in substantial, and time-consuming interaction with a very few communities or households, yet the sponsor wants an assurance that these will yield "representative" and "generalisable" results.
It is a valuable property of random selection that it tends to "balance out" various aspects of untypicality over relatively large samples: in very small samples a random selection may be obviously off-balance in important respects. The small sample will therefore most probably be chosen on a judgment basis, but note that it still cannot cover or distinguish the large range of ways in which first-stage units will vary. To choose Nepal and the Maldives as a sample of two countries on the basis that one is hilly and the other low-lying is to overlook many other features of available profile information about climate, culture, natural resources, governance and so on. The small sample of first-stage units may have to be accepted as a case study with limited capacity for generalisation. It is therefore best if it can involve primary units which are important in their own right and "well-known".
6.2 Putting small samples in context
As in 4.4 above, the in-depth study has more plausibility if it is based in a larger and more representative sample. So a relatively quick study may be carried out in a larger sample of units, with the accompanying in-depth study conducted in a systematically selected subset. There are various ways of achieving this, and thereby adding to the plausibility of a claim that the narrowly based in-depth work represents a wider reality. The following sections offer some lines of thought on this topic.
6.3 Ranked set sampling
The approach used in ranked set sampling is indicated by the simple example below which compares with taking a random sample of 5 households from a village. When the process of ranking consumes relatively little effort, procedures based on this idea can be attractive. Efficiency gains are generally good even if honest efforts at ranking are subject to some error. Ranking at random make the process no better and no worse than simple random sampling.
|
The number n = 5 above is arbitrary: the ranking task is harder for larger n, and the efficiency gain is less when n is small. It is important to use complete rounds, so the size of the sample selected is a multiple of n.
6.4 Sub-sampling
If a general study, e.g. a baseline survey, has been carried out on a relatively large random sample of the population, maybe creating a project master sample, other studies - including those with very small sample sizes - can draw from it, as long as the baseline survey members are well enough documented that they can be found again! In the same spirit as the preceding section 6.3, later-stage samples may be taken in an objectively-defined way, which allows them to be described as "representing" the original large sample.
The first-stage, baseline survey members are often post-stratified i.e. divided into meaningful categories on the basis of information collected in the baseline study. Within a stratum they may be ranked or scored on several criteria: if the results can be synthesised into an overall rank, score or categorisation, this can lead to a "sensible" and "objective", if perhaps rather arbitrary, set of rules for selecting a reasonable sample.
As a hypothetical example, one might make a case (a) to omit the top and bottom 10% of households by size, to omit all cultivators using any very unusual farming system, to omit those already participating in another time-consuming project study, then (b) to divide the remainder into strata by headship gender, by good/poor access to irrigation, etc. then (c) to select a sample from the strata. The sample selection may use the principles in 4.4.
6.5 Post hoc validation
If a detailed piece of research has been based on a small number of units, it may still lead the researcher to new insights and deeper understanding, which the researcher feels can be applied in a wider sphere. If so, the work and its conclusions can be validated by demonstrating its predictive ability: a follow-up study is devised to test key statements related to ways the researcher thinks the initial work will improve future practice. This study probably can and should be less resource-intensive and less wide-ranging in content than the original in-depth work but perhaps covering a larger sample of respondents, so it can authenticate key predictions made in advance by the researcher.
6.6 The £2 coin
Readers not resident in Britain may not appreciate this sub-section heading. Round the edge of this British coin there is the phrase, "Standing on the shoulders of giants" acknowledging debts to earlier workers. This idea is perhaps especially relevant to those with modest research resources: a couple of examples are given.
An earlier booklet in this series Project Data Archiving - Lessons from a Case Study described how a large land utilisation survey had produced substantial records for each of a large number of estates in Malawi, and an archive of these data. A future team of researchers working in the same setting should be well placed to subsample from amongst the large number of units for which 1996 data are documented. As a sampling frame, the archive data would not be wholly up-to-date or accurate, but it would be far more informative than any mere listing: sampling of estates in 1999 or 2001 would still do far better to build upon than to ignore it. The existence of good-quality data from some years earlier can be of considerable value in looking at change through time with an eye to issues such as monitoring and impact assessment, sustainability or biodiversity loss.
Research currently underway in Uganda involves establishing a series of Benchmark Sites for banana research. These sub-county sized "primary units" will be well-documented: projects working in any of the sites will effectively be able to buy into shared baseline studies, and save a great deal of time and money, as well as having a more than usually effective sampling frame.
[TOP]
7. Where is the recipe for me to follow?
The above notes attempt to illustrate a range of concepts which researchers can utilise in the course of thinking out how a set of sampling procedures fits into their research strategy. These concepts have been selected from a larger range as being important, relevant and susceptible to non-technical description. They are not intended to produce sophisticated schemes, or definitive data: this is usually very difficult and expensive to do even for well-resourced projects in well-favoured areas in developed countries.
The development researcher often has to use great intelligence and ingenuity to conceptualise and operationalise a research idea, in a difficult setting with limited resources and limited information to hand. Sampling is one of the aspects where just such ingenuity has to be applied to suit the research setting; just as it would be laughable to suggest that all research projects should conform to one format, so it would be foolish to demand a fixed sampling plan which ignored project circumstances.
Making your own sampling decisions based on careful thought and detailed planning is a positive challenge: dialogue with some people experienced in sampling issues is often a great help to ensure the proposal covers all the necessary issues in a sensible way, and we would advocate that at least one of them should be a sympathetic statistician. Even if experience shows you that your solution is less than perfect, you can take comfort from knowing the alternative is worse: adopting pre-packaged solutions and standard plans without thought would probably be a recipe only for disaster!
[TOP]
Last updated 11/04/03