Mixed Models & Multilevel Data Structures in Agriculture
Release date: April 2001>
This is one of a series of guides for research and support staff involved in natural resources projects. The subject-matter here is mixed models and multilevel data structures in agriculture. Other guides give information on allied topics.
Contents
1. Introduction
2. Examples
3. Mixed Models and Data Structure
4. Example 1: Fodder production trial
5. Example 2: Concentrate feeding trial
6. Example 3: Sheep breeding trial
7. And finally...
Appendix: Balanced Split-plot ANOVA for the 14-week forage dry matter data from the fodder production trial of Example 1
Acknowledgements
This guide was written by Eleanor Allan (SSC) and John Rowlands (ILRI, Nairobi).
We are grateful to ILRI, and in particular to scientists Leyden Baker, Dannie Romney and Joseph Methu, for permission to use the data from their work.
Comments on earlier drafts were made by Ric Coe (ICRAF, Nairobi), Joris De Wolf (ERM, Brussels), and Savitri Abeyasekera and Roger Stern (SSC, Reading). We are grateful for their contributions.
1. Introduction
Hierarchical or multilevel data structures can occur in many areas of agricultural research - for instance in on-farm trials, where there can be information at the village, farm and plot or animal level. Experiments in animal breeding are often concerned with attributing variation in traits of offspring, such as their growth, to the sires and dams from which they were bred. Researchers in this discipline are therefore familiar with the idea that livestock data often have some hierarchical structure with different levels of variation.
Analysis of variance - except in balanced or nested designs - has been difficult to apply to data with a multilevel structure. Mixed modelling is becoming a standard approach for analysing these types of data, particularly since it can deal with complicated or "messy" structures. The mixed model facilities are now available in some of the more powerful statistical packages such as Genstat and SAS.
There seems to be some "mystique" surrounding these methods, and our claim is that there should not be. The purpose of this guide is to review the general concepts of mixed models. We illustrate by example how to recognise the structure in the data and how to fit and interpret a mixed model analysis. The reader is expected to be familiar with simple analysis of variance methods.
[TOP]
We use three examples. Example 1 is a fairly traditional agricultural experiment, and is included to show how mixed modelling links to more traditional analyses. Example 2 is an on-farm trial with a slightly "messy" hierarchical structure. We use it to show how the ideas of example 1 can be extended to other situations, and to demonstrate the benefits of mixed modelling. Example 3 is a more specialised example of a breeding trial; with it we discuss the implications of formulating models in different ways.
Example 1: Fodder production trial
Example 2: Concentrate feeding trial
Example 3: Sheep breeding trial
Example 1: Fodder production trial
In the Central Kenya Highlands, where maize is the most important staple, the availability of fodder is a major constraint on livestock production. It has been suggested that maize thinnings be used as animal fodder. A randomised complete block experiment, with six blocks of three main plots of approximately equal size, was carried out at a local farm to investigate different planting densities and thinning methods. The objective was to identify a practice that would increase forage production without compromising the harvest grain yield for human consumption (Methu et al., 2001).
Maize was planted using densities of two, three or four seeds per hole, and planting density was randomised to the plots such that there was one plot of each planting density per block. Spacing between holes was the same for all plots.
Thinning was carried out on plots planted with more than two seeds per hole - at 8 and 14 weeks for the plots with four seeds per hole, and at 14 weeks for the plots with three seeds per hole - so that from 14 weeks onwards all plots had two seeds per hole. There were also two thinning practices: the removal of the smallest plant from the hole, and the removal of the second largest plant from the hole. To incorporate this into the experiment, the three- and four-seed plots were subdivided into two and these two sub-plots were randomly allocated to one of the different thinning practices. The two-seed plot was not subdivided.
At weeks 8 and 14 the amount of green forage (kg/ha of Dry Matter) was recorded for the plots which were thinned. At the end of the study, at week 28, grain yield (also in kg DM/ha) was determined for all plots.
Example 2: Concentrate feeding trial
Dairy production is an important source of income for many smallholder households in the highlands of East Africa. The large majority of farmers feed a low, flat rate of concentrate to their cows throughout lactation. This is primarily because of cash flow problems and not being able to pay for concentrates ahead of having milk to sell. The data used in this example are from a pilot study of small-holder farmers in Kiambu district in Central Kenya. The aim was to test the feasibility of changing farmers' concentrate allocation practice by shifting the concentrates to early lactation. This was to be achieved by arranging for their farm cooperative to allow them extra credit at the beginning of a cow's lactation(Romney et al., 2000). The data comprised weekly records of milk yields and concentrates offered for the first 12 weeks of lactation, and approximately fortnightly thereafter. Data were collected between March 1999 and March 2000, and complete datasets were achieved for 65 cows belonging to 53 households and calving between March and September 1999.
The objective of the analysis described here is to determine (a) the influence of household (farm) and cow factors on milk yield, and (b) the relationships between milk yield and concentrate fed at different phases of lactation. Five six-week sampling periods up to 30 weeks of lactation were defined, and average daily milk yield (kg/day) in these six-week intervals was estimated for each animal from fitted lactation curves.
Example 3: Sheep breeding trial
Helminths constitute one of the most important constraints to livestock production in the tropics. Breeding for disease resistance may be one solution. The data used in this example are from a study on the Kenya coast between 1991 and 1997 (Baker, 1998). The purpose of the experiment was to compare the genetic resistance to helminthiasis of two indigenous breeds of sheep - Dorper and Red Maasai - and to use this information alongside survival rate to compare the overall productive performance of each breed.
Throughout the six years, Dorper (D), Red Maasai (R) and RxD ewes were mated to Red Maasai and Dorper rams to produce a number of different lambs genotypes. For the purposes of this example, however, only the following four offspring genotypes are considered: DxD, DxR, RxD and RxR. These comprised 882 lambs born to 74 sires and 367 ewes. Thus, each ewe gave birth on average to more than two lambs, each in a different year.
Data on aspects of growth and survival were collected on the lambs. Here, for the purpose of demonstration, we consider just the body weight (kg) at weaning of 700 lambs that survived to weaning with the objective of determining the differences in growth between breeds to this time.
[TOP]
3. Mixed Models and Data Structure
Mixed model methodology (also known as REML analysis, where REML stands for residual, or restricted, maximum likelihood) takes its name from the fact that the elements of the model underlying the analysis can be a mixture of what are called fixed and random effects. Below we explain these different components of a mixed model, and show how mixed modelling can deal with the analysis of data from multilevel structures.
3.1 Fixed and Random Effects
3.2 Multilevel Structure
In describing variation in data, an effect is some characteristic or trait which is known - or thought - to have some impact on the measured result, such as weaning weight of lambs.
Experimental treatments are often - though not always - fixed effects. The different planting densities of example 1 would be one such example. The three planting densities were specifically chosen for investigation in order to quantifying the differences, if any, amongst them. Fixed effects are summarised by means and standard errors.
Another example of a fixed effect would be the sex of the offspring lambs in the breeding experiment. Whilst it is not an effect which can be specifically designed into the study, we should nevertheless want to quantify the difference in growth between males and females.
In contrast, the influence of the ram on the growth of its offspring in a breeding experiment is usually a random effect, since the researcher is interested in quantifying how much variability in the growth is due to the sire of the lamb, as opposed to comparing individual rams within the experiment itself. Random effects are summarised by variances.
By defining an effect as random, we are visualising the set of units under investigation as a representative sample from a wider population. Thus, in the breeding example, the rams whose offspring are under investigation are regarded as randomly selected members of all rams belonging to a particular breed.
In multilevel data structures there are different types of investigational units at different layers - e.g. plots within farms, or animals within herds - and attributes associated with these different units whose effects we wish to assess - e.g. planting density, thinning practice, breed or sex of the animal. We refer to "investigational units" or "units" throughout the guide in order to generalise our mixed model concepts to the analysis of data from experiments, surveys and observational studies, where such terms as experimental, sampling and observational units might be found.
The response of interest, such as crop yield or weaning weight, is usually measured at the lowest layer, but the variation in these responses is due to variability at the different layers. For example variation in crop yields collected in an on-farm trial is partly due to farm-to-farm variability and partly to plot-to-plot variability. To incorporate these different levels of variability into our mixed model for hierarchical data, we specify the units in the layers as random effects.
The attributes of the units (e.g. planting density) are usually fixed effects. By correctly identifying which attributes occur at each layer, the mixed model can extract the residual, unexplained, variation within the layers, which is necessary for determining the precision of the comparisons of the attributes. This idea is similar to the split-plot ANOVA which has two parts, a main plot part and a sub-plot part, each with its own residual variance, and where the main plot and sub-plot treatment factors are tested at their relevant level.
By specifying the units in a layer as random, we assume that, within a layer, the units are "independent" of one another. This means that, in the fodder production trial for instance, after allowing for differences amongst the blocks, there is no correlation between the yields in different plots within a block.
Correctly identifying the layers in the data, and the different characteristics or attributes associated with them, is crucial to successful modelling of multilevel data. To help recognise the structure in data we use what we describe as a "mixed model tree" to develop the different layers pictorially. We hope this tool will help researchers identify the hierarchical structures of their data and consequently formulate and interpret a mixed model analysis.
[TOP]
4. Example 1: Fodder Production Trial
4.1 Recognising the Structure
4.2 Analysis
4.1 Recognising the Structure
The figure below depicts the full mixed model tree for this first example. To the left we describe the layers, and to the right the characteristics of the experimental material which can be attributed to the different layers. Since the layout is the same within each block, detailed layering is shown for only one block in the tree.
The six blocks describe the way the experiment was laid out - they thus represent the top layer. Each block was divided into three main plots, represented by the small boxes within the larger box. This is the second layer, the one at which the three planting density treatments are randomised, as shown on the right of the diagram.
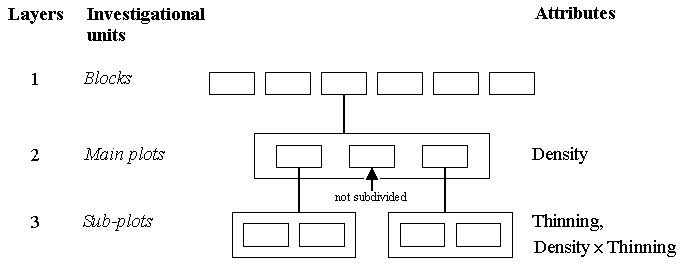
Two of the main plots (with 3 and 4 seeds per hole), but not the one with 2 seeds per hole, are subdivided into two sub-plots, so the sub-plots constitute the third layer of investigational units. Method of thinning is randomised to these sub-plots, and so the actual treatments applied to the sub-plots are combinations of planting density and thinning practice. Method of thinning is, therefore, an effect at this lower level, as is the density x thinning interaction.
The above diagram represents the structure of the data on grain yield collected at the end of the experiment when the crop was harvested. As the tree shows, yield data are collected from one main plot (2 seeds per hole) and from four sub-plots (3 and 4 seeds per hole).
For the green forage yield data collected at 14 weeks, however, there are only two main plots per block, since no thinning is carried out on the plots planted with 2 seeds per hole. Plots planted with 3 or 4 seeds per hole are thinned at 14 weeks - yield data are all from the four subplots in a block, and so the mixed model tree becomes:
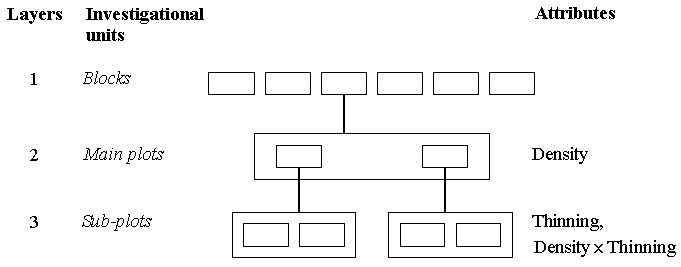
The above multilevel data structure at 14 weeks is that of a balanced split-plot experiment - there are yield data for each of the two sub-plots from each of the two main plots per block. These data would normally be analysed by a simple split-plot analysis of variance. However, they can also be analysed as a mixed model, as we shall see later.
The green forage yield data collected at 8 weeks are only collected for the main plots with 4 seeds per hole, and so the mixed model tree simplifies even further. There are now only two layers in these data - blocks and sub-plots to which thinning treatments are randomised. With only one main plot per block, the main plot effect cannot be distinguished from the block effect. This is just a randomised block structure, with two units per block. We will not consider these data further.
4.2 Analysis
The Genstat output for the mixed model analysis of the 14-week green forage yields is presented in Figures 1(a) to 1(c) below. Since this data set is a balanced split-plot experiment it would normally be analysed by analysis of variance; and so, for interest, and so that the reader can see the transition from analysis of variance to mixed modelling, this approach is also presented in the Appendix.
Figure 1(a)
***** REML Variance Components Analysis *****
Response Variate : Forage14
Fixed model : Constant+density+thinning+density.thinning
Random model : block+block.mainplot+block.mainplot.subplot
Number of units : 24
Figure 1(a) summarises the mixed model specification in Genstat, with a brief explanation of the Genstat syntax. Block, main plots within blocks and sub-plots within main plots are declared to be random effects - thus setting up the hierarchical structure - whilst planting density, thinning and the density x thinning interaction are all fixed effects. The important point to note is that the different layers in the data must be specified in the "random model" correctly. The software is then able to work out from this and the layout of the data in the data file how to attach each attribute in the "fixed model" to the different layers, so that the user does not have to be so concerned about this. The results of the analysis are shown in Figure 1(b).
Figure 1(b)
*** Estimated Variance Components ***
Random term Component S.e.
block 17860. 42962.
block.mainplot 39912. 51098.
block.mainplot.subplot 73238. 32753.
*** Approximate stratum variances ***
Effective d.f.
block 224501. 5.00
block.mainplot 153062. 5.00
block.mainplot.subplot 73238. 10.00
*** Wald tests for fixed effects ***
Fixed term Wald statistic d.f.
density 0.1 1
thinning 15.7 1
density.thinning 0.0 1
* All Wald statistics are calculated ignoring terms fitted later in the model
The first point to notice from Figure 1(b) is that although the degrees of freedom for each of the fixed effects of planting density, thinning and density x thinning are as one would expect, the significance tests provided by Genstat for these effects are now Wald tests, and not the F-tests we are used to with analysis of variance.
The
Wald tests in the mixed model framework investigate the same hypotheses
as the F-tests in the split-plot analysis of variance - i.e.
null hypothesis of no effect - but unlike the F-statistics,
which follow an exact F-distribution, the Wald test statistics
follow a Chi-squared (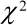
) distribution, but only approximately.
The main points to be aware of are that (a) the validity of the
Wald testing depends on the sample size being large enough (the
sample size is quite small in this example), and (b) the tests are
more liberal than the F-tests, with the significance levels
of the two becoming more similar with increasing sample size.
In
our example, the significance level for the comparison of methods
of thinning is p=0.003 in the split-plot ANOVA. This compares
with p<0.001 for the Wald value of 15.7 found by a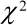
test with 1 degree of freedom. Both methods give similar conclusions:
there is no effect of planting density on the 14-week green forage
yield regardless of which plant is thinned (Wald statistic of 0.1),
but the yields differ significantly as a result of different thinning
practices.
The second point to notice is that the stratum variances, and their associated degrees of freedom, in the mixed model output are the same as the residual mean squares in the three strata in the analysis of variance output. These stratum (or layer) variances are estimates of the variation among blocks, among main-plots within the blocks and between subplots within the main-plots. Just like the residual mean squares in the ANOVA table, they are concerned with the variability in the yield data summarised at each layer.
The mixed model analysis also gives estimated variance components. In traditional designed experiments these are usually of little interest, and so tend not to be presented as part of the ANOVA output. There are instances, however, when these components are of interest in their own right, and we return to this idea in the third example.
Finally the mixed model gives us estimates of treatment means - referred to in Figure 1(c) as 'predicted means' - and standard errors of differences. These are identical to the corresponding values in the split-plot analysis of variance shown in the Appendix.
Figure 1(c)
*** Table of predicted means for density ***
density 3 4
1455 1397
Standard error of differences: 159.7
*** Table of predicted means for thinning ***
thinning L S
1645 1207
Standard error of differences: 110.5
*** Table of predicted means for density.thinning ***
thinning L S
density
3.00 1663 1248
4.00 1627 1167
Standard error of differences for same level of factor:
density thinning
Average 156.2 194.2
Maximum 156.2 194.2
Minimum 156.2 194.2
As stated before, data from a balanced split-plot experiment are usually analysed using a split-plot analysis of variance. Above we have shown that this approach is just a simple example of a mixed model. Therefore either method could be used. Many multilevel structures though are not balanced - as is often the case in on-farm trials - and there is then no analysis of variance equivalent to the split-plot ANOVA; in such cases researchers need to move to mixed modelling.
The aim of this trial was to see whether there could be increased forage yield for livestock without affecting grain yield at harvest for human consumption. Below we consider the analysis of the grain yield, but only selected parts of the output are presented in Figure 1(d); the Genstat commands to request the analysis are the same as before and are not given.
The data structure is no longer balanced in the sense that, since thinning took place on only two of the three planting density plots, grain yields are available for one main plot and for four sub-plots per block. The mixed model successfully takes this into account, as can be seen from the degrees of freedom for the fixed effects. As before, there are 2 degrees of freedom for the planting density main effect (since it is possible to compare all three densities at the main plot level) and 1 degree of freedom for the thinning main effect. For the density x thinning interaction though there is only 1 degree of freedom, since we now compare the difference between the two thinning practices for only two planting densities.
The unbalanced structure is also responsible for the degrees of freedom for the stratum variances now being "effective" values of 9.79 and 10.21 (instead of 10 and 10).
Figure 1(d)
*** Approximate stratum variances ***
Effective d.f.
block 566532. 5.00
block.mainplot 206946. 9.79
block.mainplot.subplot 94098. 10.21
*** Wald tests for fixed effects ***
Fixed term Wald statistic d.f.
density 1.0 2
thinning 3.1 1
density.thinning 3.1 1
* All Wald statistics are calculated ignoring terms fitted later in the model
*** Table of predicted means for density.thinning ***
thinning 0 S L
density
2 2126 * *
3 * 2494 2054
4 * 2338 2338
Standard error of differences: Average 222.4
Maximum 233.7
Minimum 177.1
Average variance of differences: 49958.
Standard error of differences for same level of factor:
density thinning
Average 177.1 233.7
Maximum 177.1 233.7
Minimum 177.1 233.7
The analysis demonstrates no effect of density of planting (with subsequent removal of one or two plants) on harvested grain yield. Furthermore, removal of the second largest rather than the smallest plant did not appear to significantly reduce grain yield (the Wald
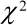statistic needs to exceed 3.84 to represent a significant effect at
the 5% level).
Further information on the analysis of a split-plot experiment may be found in textbooks such as Statistical Methods in Agriculture and Experimental Biology by Mead, Curnow and Hasted (1994, Chapman & Hall, London).
SAS users may like to note that the SAS system also gives approximate F-tests in its mixed models procedure. In terms of model development, both are equally useful.
[TOP]
5. Example 2: Concentrate feeding trial
5.1 Recognising the structure
5.2 Analysis
5.1 Recognising the structure
The objective here was to look at the effects of various factors on milk yield collected over different sampling periods from cows at several farms. Exploratory analysis of the data indicated that farm income, cow size (as determined by measurement of its heart girth) and season of lactation could be important explanatory variables. Milk yield was also thought to vary with phase of lactation and to be linearly related to the level of concentrate fed.
There are three layers of investigational units in our mixed model tree, namely farm, cow within farm, and sampling period within cow. Sampling periods are more difficult to visualise as a random effect than farm or cow in view of their serial nature. They do, however, represent a layer of within cow variation, and need to be taken into account in the hierarchical structure of the data. We assume here the usual assumption of independence amongst the sampling periods. This is an example of repeated measurement data, to which we will return at the end of this section.
Almost all farms had either one or two cows, and each cow provided milk yield for no more than the five sampling periods. To illustrate this we have shown the layering at two farms, one with two cows and one with only one; and layering for two cows, one with 5 sampling periods and one with 4 periods.
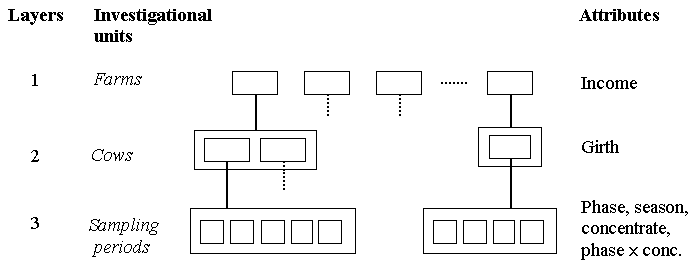
Farm income is clearly an attribute of the farm, and heart girth an attribute of the cow. The sampling periods can be characterised by the season when sampling occurs and the phase of lactation. The level of concentrate fed varied in the different sampling periods and is therefore an effect at the sampling period layer, as is the phase x concentrate interaction.
5.2 Analysis
The Genstat model specification is given in Figure 2(a). Fixed effects are farm income (classified into 6 categories), heart girth and average concentrate fed, as covariates, and phase of lactation and season of lactation, each with 5 levels, as factors. The interaction between phase of lactation and concentrate fed is also included. Random effects are farm, cow within farm and sampling period within cow.
Figure 2(a)
***** REML Variance Components Analysis *****
Response Variate : milk
Fixed model : Constant+income+girth+phase+season+avconc+phase.avconc
Random model : farm+farm.cow+farm.cow.sampling
Number of units : 289
*** Estimated Variance Components ***
Random term Component S.e.
farm 5.649 3.815
farm.cow 8.092 3.413
farm.cow.sampling 2.575 0.251
*** Approximate stratum variances ***
Effective d.f.
farm 64.676 48.97
farm.cow 36.362 13.02
farm.cow.sampling 2.575 211.01
*** Wald tests for fixed effects ***
Fixed term Wald statistic d.f.
income 7.9 1
girth 28.0 1
phase 267.2 4
season 13.8 4
avconc 3.7 1
phase.avconc 18.2 4
* All Wald statistics are calculated ignoring terms fitted later in the model
From the analysis in Figure 2(a), each of the Wald statistics shows some degree of significance, except perhaps the term for average concentrate. (As mentioned earlier, Wald statistics follow approximately a Chi-square distribution with
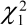and 
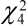= 3.84 and 9.49 respectively,
at the 5% significance level). But one must be careful. The data structure
here is quite clearly unbalanced. There are different numbers of cows
within the farms and different numbers of sampling periods for the
different cows. When data are unbalanced
the order in which fixed effects are included and tested is important.
Figure 2(b)
*** Table of effects for income ***
0.7689 : standard error 0.4904
*** Table of effects for girth ***
0.2635 : standard error 0.05479
*** Table of effects for avconc ***
-0.2142 : standard error 0.1426
*** Table of effects for phase.avconc ***
phase
1-6 0.0000
7-12 0.6148
13-18 0.5637
19-24 0.3339
25-30 0.6792
Standard error of differences: Average 0.1913
Maximum 0.2269
Minimum 0.1614
*** Table of predicted means for phase ***
phase 1-6 7-12 13-18 19-24 25-30
14.49 14.56 13.05 11.24 9.92
Standard error of differences: Average 0.3732
Maximum 0.4531
Minimum 0.3049
*** Table of predicted means for season ***
season M-M J-J A-O N-D J-M
13.10 11.84 12.09 12.81 13.42
Standard error of differences: Average 0.4338
Maximum 0.5632
Minimum 0.3209
A second point to note also relates to the "messy" structure of data. Most farms (42) in the study only had one cow, 10 farms had 2 cows and one farm had 3 cows. The experimental design of example 1 was completely balanced in a way that allowed the information on each attribute to be retrieved exclusively from the layer at which it was defined. In this example here, because of the large amount of confounding between farm and cow, the information on the effect of heart girth comes both from the cow layer and the farm layer, (i.e. farms where there is only one cow). In these situations mixed model analysis combines all the relevant information from different levels to produce estimates of effects and standard errors. This ability to extract and combine information from different levels, and attach a correct measure of precision to the estimates, is what makes mixed modelling so useful. A consequence, however, is that exact significance tests of hypotheses are no longer possible, and we depend more on the large sample properties needed for the Wald tests.
The analysis shows that level of milk yield was positively related to the size of the cow (heart girth), though, because of the confounding between cow and farm, this may be more a characteristic of farm management than the cow itself. Milk yield varied with season and was reduced between June and October (the second two seasonal periods, J-J and A-O). It also decreased from an average of 14.5 kg/d during the first 12 weeks of lactation to 9.9 kg/d between 25 and 30 weeks. The effect of concentrate on milk yield within cow was positive only during phases 2 to 5 of lactation. This is reflected in the significant phase x concentrate interaction.
We return briefly to the issue of repeated measurements. Earlier we introduced the idea that the units within a layer were "independent" of one another. With repeated measurements - as in our sampling periods - this may not be true. When measurements are collected successively within an individual unit, they are often correlated - with higher correlation between measurements that are close together in time and lower correlation between measurements that are further apart. There are further facilities within mixed modelling to handle repeated measurement structures, but they are beyond the scope of this guide.
Each Wald statistic is calculated adjusting for those effects already included in the model, but ignoring those to follow. For a full analysis of these data, one would want to fit several models with the fixed effects specified in different orders.
[TOP]
6. Example 3: Sheep breeding trial
6.1 Recognising the Structure
6.2 Analysis
6.1 Recognising the Structure
In this example we compare the performance of lambs of Dorper and Red Maasai breeds and their crosses, in terms of just one trait - weaning weight. Preliminary analysis of the data indicated that the lamb's sex and its age at weaning were likely to influence weaning weight, as were the breed of the ram and the ewe. The age of the ewe was also thought to influence the growth of a ewe's offspring.
Both rams and ewes were each selected at 'random' from two breeds, and mated to produce their offspring. Since the selections of ram and ewe were made in parallel, both can be represented as investigational units at a top layer. Breeds for each sex are attributes at these two top layers, while age of ewe is also an attribute at the ewe layer.
In the mixed model tree below, we have attempted to show that there were more ewes than rams, that each ram mated with several ewes, and that there was only one offspring for any one mating.
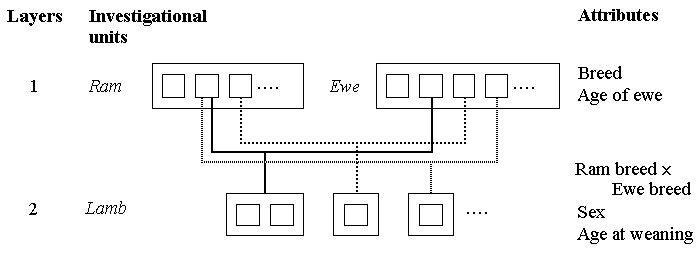
The offspring lambs are the investigational units at the next layer down. Their attributes include sex and age at weaning. Since rams and ewes are mated both within and across breeds to produce their offspring, the interaction of ram breed and ewe breed is also at this level.
6.2 Analysis
The effects of individual rams and ewes on offspring growth are defined as random effects - the remaining effects are fixed. Preliminary analysis suggested that the effect of the age of a ewe on the weaning weight of its offspring was curvilinear and could be represented by a quadratic function. Weaning age was linearly related to weaning weight. The Genstat specification of these fixed and random effects is given below in Figure 3(a).
Figure 3(a)
***** REML Variance Components Analysis *****
Response Variate : weanwt
Fixed model : Constant+year+dam_ageL+dam_ageQ+wean_age+sex+ram_brd+ewe_brd+
ram_brd.ewe_brd+year.ram_brd
Random model : ram+ewe/lamb
Number of units : 700
Figure 3(b)
*** Estimated Variance Components ***
Random term Component S.e.
ram 0.059 0.089
ewe 1.473 0.286
lamb 3.430 0.268
*** Approximate stratum variances ***
Effective d.f.
ram 4.654 56.07
ewe 6.505 297.43
lamb 3.430 328.49
*** Wald tests for fixed effects ***
Fixed term Wald statistic d.f.
year 231.4 5
dam_ageL 31.0 1
dam_ageQ 85.2 1
wean_age 59.7 1
sex 6.2 1
ram_brd 6.8 1
ewe_brd 2.9 1
ram_brd.ewe_brd 0.5 1
year.ram_brd 4.5 5
* All Wald statistics are calculated ignoring terms fitted later in the model
The Wald statistics in Figure 3 (b) demonstrate the highly significant fixed effects of year of birth, age of dam (described by linear and quadratic terms dam_ageL and dam_ageQ, respectively), age at weaning and, to a lesser extent, sex on weaning weight. As in the last example, the reader should note that these data are unbalanced, and so each Wald statistic corrects for terms already fitted but not those that follow. The breed of the ram appeared to play a more significant effect then the breed of the dam on weaning weight and there was no variation in the effect with year.
Figure 3(c)
*** Table of effects for dam_ageL ***
2.338 : standard error 0.2345
*** Table of effects for dam_ageQ ***
-0.2893 : standard error 0.03192
*** Table of effects for wean_age ***
0.06694 : standard error 0.008690
*** Table of predicted means for year ***
year 91 92 93 94 95
12.64 11.06 11.55 9.65 9.44
year 96
10.19
Standard error of differences: Average 0.3280
Maximum 0.4007
Minimum 0.2591
*** Table of predicted means for sex ***
sex F M
10.55 10.96
Standard error of differences: 0.1629
*** Table of predicted means for ram_brd ***
ram_brd D R
10.98 10.53
Standard error of differences: 0.1830
*** Table of predicted means for ewe_brd ***
ewe_brd D R
10.99 10.52
Standard error of differences: 0.2722
*** Table of predicted means for ram_brd.ewe_brd ***
ewe_brd D R
ram_brd
D 11.08 10.88
R 10.89 10.17
Standard error of differences: Average 0.3163
Maximum 0.3530
Minimum 0.2578
*** Table of predicted means for year.ram_brd ***
ram_brd D R
year
91 12.96 12.31
92 11.62 10.50
93 11.67 11.44
94 9.62 9.67
95 9.75 9.12
96 10.24 10.14
Standard error of differences: Average 0.4510
Maximum 0.5602
Minimum 0.3423
The table of effects (for regression coefficients for covariates) and means, in Figure 3(c), demonstrates the lower values of weaning weight in 1994, 1995 and 1996 compared with the other years. Male lambs had slightly higher weaning weights than females. Breed differences were similar for both sexes but the standard error was higher for ewes than rams.
Earlier we introduced the idea that variability in individual response data - in this case weaning weight - comes from the different layers in a hierarchical structure. Mixed modelling estimates the components coming from each source. These variance components have an important understanding to animal and plant breeders because they provide the basis for calculating genetic parameters such as heritability. In this example the ewe variance component, shown in Figure 3(b), is much higher than the ram component indicating the maternal influence on growth to weaning. The 'genetic' variation in lamb weaning weight is therefore primarily associated with the lamb's dam.
For the three examples we have used the idea of random effects solely to incorporate the layers into our mixed models. Sometimes we also want to declare an attribute of interest, such as year of birth, as random rather than fixed. Why should we do this, and what implications does it have on the analysis?
If such an effect is defined as random, then any interaction involving it and any other effect, fixed or random, will also be random. For instance when year is declared random, the random breed x year interaction is the random variation of the breed effects across the years. Within the mixed model, the average breed effects are then compared with these year-to-year breed differences. Consequently the Wald statistics are usually smaller than in the fixed effects model, and the standard errors of the estimates are larger. Our inferences about the breeds are then for a population of years which our sample represents.
The analysis with year taken as random is shown below in Figure 3(d). Since the breed x year interaction was negligible, similar results were obtained to those shown in Figure 3(c) above. Whilst the choice of whether an effect should be fixed or random depends on the interpretation that the researcher wants to put on his analysis, it must also depend on whether or not it is sensible to visualise the effect as a random sample from some much larger population. In this example, where there are only 6 years, one might want to consider whether that sample is large, or long, or random enough to be representative of the wider population of time.
The difference between declaring an effect as fixed or random depends on the inferences one wants to make. In the above example, when year was a fixed effect, inferences about the performance of the breeds related to the six years in question. To generalise conclusions about breed effects to a much wider time spectrum, then year and the year x breed interaction must be in the model as random effects. The other situation where attributes are commonly taken as random is when an effect, such as a blocking factor, e.g. herd, has many levels, and summarising it in terms of a variance seems justified. In such instances treating the effect as random, rather than fixed, often makes the model easier to fit.
Figure 3(d)
***** REML Variance Components Analysis *****
Response Variate : weanwt
Fixed model : Constant+dam_ageL+dam_ageQ+wean_age+sex+ram_brd+ewe_brd+
ram_brd.ewe_brd
Random model : ram+ewe/lamb+year+year.ram_brd
Number of units : 700
*** Estimated Variance Components ***
Random term Component S.e.
ram 0.077 0.091
ewe 1.456 0.284
year 1.447 0.950
year.ram_brd 0.000 0.055
lamb 3.427 0.267
*** Approximate stratum variances ***
Effective d.f.
ram 4.841 58.07
ewe 6.481 297.85
year 219.589 4.80
year.ram_brd 3.458 0.97
lamb 3.427 330.31
*** Wald tests for fixed effects ***
Fixed term Wald statistic d.f.
dam_ageL 30.2 1
dam_ageQ 84.4 1
wean_age 61.2 1
sex 6.1 1
ram_brd 6.5 1
ewe_brd 4.0 1
ram_brd.ewe_brd 0.6 1
* All Wald statistics are calculated ignoring terms fitted later in the model
[TOP]
7. Non-Parametric Methods
The normally distributed measurement is the starting point of much statistical analysis. There are situations where this seems worryingly inappropriate. Measurements are perhaps from a very skew distribution, where an occasional reading is much larger than the usual range and cannot be explained or discounted. Results may be only quasi-numerical, e.g. an importance score between 1 and 10 allocated to several possible reasons for post-harvest fish losses. Different fishermen may assign scores in their own way, some avoiding extreme scores, while others using them. We may then have reasonable assurance as to the rank order of scores given by each individual, but doubtful about applying processes such as averaging or calculating variances for scores given to each reason.
In
such cases it is sensible to consider using non-parametric methods.
A simple example is the paired data shown earlier in Section
5.1. Here the ten differences in breaking strength were as follows:
3 2 3 1 3 0 3 1 1 1
Earlier we used the t-test, but a simple non-parametric test
follows from the fact that nine out of the ten values are positive,
with the other being zero. If there were no difference in the before
and after reading we would expect about half to be positive and
half negative, so this simple summary of the data provides good
evidence (p = 0.004, on a formal test) against this hypothesis.
Just noting whether the observations are positive, zero or negative
is also clearly robust against occasional readings being very large
- if the first difference were 30, rather than 3, this would not
affect the analysis. Thus non-parametric methods often provide a
simple first step. They also add easily explained support for the
conclusions from a parametric analysis.
We advise caution, however, about the over-use of non-parametric methods. Inadequate understanding of the data-generating system by the researcher may be the real reason for messy-looking data. A common reason for apparently extreme values, or lumpy distribution of data, is often that the population sampled has been taken as homogeneous, when it is an aggregate of different strata, within which the observations follow different patterns.
Sometimes problem data arise from poorly designed measurement procedures, where a more thoughtful definition of raters' tasks would produce more reliable data. It is then better to think harder about the structure of the data than to suppress the complications and use an analysis that ignores them.
The ethos of non-parametric methods often stems from assuming the measurements themselves are flawed, or at least weak, so that estimation procedures are of secondary importance. The primary focus of most non-parametric methods is on forms of hypothesis testing, whereas the provision of reasonable estimates usually generates more meaningful and useful results.
In the final section of this guide we outline a more general framework for the analysis of many sets of data that used previously to be processed using non-parametric methods.
[TOP]
7. And finally...
Throughout this guide we have restricted discussion on mixed modelling in agriculture to the most obvious situation of messy multilevel structures. However, the methodology is very powerful and can be used in a range of other situations - we have already mentioned repeated measurements as one example. Here we briefly discuss some of the strengths and limitations of the mixed model approach.
One strong reason for using mixed modelling is that it can deal effectively with layers in the data, and can give more valid, though theoretically approximate, significance tests and standard errors - something that conventional analysis of variance methods cannot do except in one or two specific circumstances.
Secondly, it has the ability, with unbalanced structures, to combine information from different layers in the data. (Readers who are familiar with the analysis of lattice designs, will recognise that this is akin to "recovering inter-block information".) This has the added advantage of improving the precision of fixed effects comparisons such as the experimental treatments or other covariates.
The one slight drawback of the model is that initially it seems relatively complex compared to analysis of variance. For a start, the model is more difficult to specify - one needs to correctly identify which effects are random and which are fixed. The resulting computer output is also less familiar and less easy to use than ANOVA outputs. However, researchers who are familiar with split-plot analysis of variance will probably have less difficulty with formulating the model, since the principles of identifying more that one layer of variation in the data is the same.
In conclusion, we have introduced the idea of the mixed model tree as an aid to identifying hierarchical data structure. Then, when there is such a structure, we have shown how to request the appropriate mixed model analysis. It is our hope that an understanding of the contents of this guide may lead to a better ability on the part of the reader to recognise the correct analysis. Finally a clear awareness at the planning stage of the different layers in a proposed study can help to ensure that the resulting design has sufficient replication at each layer.
[TOP]
from the fodder production trial of Example
The output below shows the appropriate split-plot analysis of variance for the two layers of the variation in the experiment and means and standard errors of differences between means.
BLOCK block/mainplot/subplot
TREATMENTS density*thinning
***** Analysis of variance *****
Variate: Forage14
Source of variation d.f. s.s. m.s. v.r. F pr.
block stratum 5 1122505. 224501. 1.47
block.mainplot stratum
density 1 20592. 20592. 0.13 0.729
Residual 5 765310. 153062. 2.09
block.mainplot.subplot stratum
thinning 1 1148000. 1148000. 15.67 0.003
density.thinning 1 3060. 3060. 0.04 0.842
Residual 10 732379. 73238.
Total 23 3791847.
***** Tables of means *****
Variate: Forage14
Grand mean 1426.
density 3. 4.
1455. 1397.
thinning S L
1207. 1645.
density thinning S L
3. 1248. 1663.
4. 1167. 1627.
*** Standard errors of differences of means ***
Table density thinning density
thinning
rep. 12 12 6
s.e.d. 159.7 110.5 194.2
d.f. 5 10 9.81
Except when comparing means with the same level(s) of
density 156.2
d.f. 10
References
Romney, D., Kaitho, R., Biwott, J., Wambugu, M., Chege, L., Omore, A., Staal S., Wanjohi, P. and Thorpe, W. (2000). Technology development and field testing: access to credit to allow smallholder dairy farmers in central Kenya to reallocate concentrates during lactation. Paper presented at the 3rd All Africa Conference on Animal Agriculture and 11th Conference of the Egyptian Society of Animal Production, 6-9 November, 2000, Alexandria, Egypt.
Baker, R.L. (1998). A review of genetic resistance to gastrointestinal nematode parasites in sheep and goats in the tropics and evidence for resistance in some sheep and goat breeds in sub-humid coastal Kenya. Animal Genetic Resources Information (FAO) 24: 13-30.
Methu, J.N., Owen, E., Tanner, J.C. and Abate, A.L. (2001). The effect of increasing planting density and thinning on forage and grain yield of maize in Kenyan smallholdings. ILRI.
[TOP]
Last updated 16/04/03