Statistical Good Practice Guidelines

The Statistical Background to ANOVA

by Professor S C Pearce, asru, University of Kent at Canterbury
adapted by the Statistical Services Centre

Release date: March 2000

This is one of a series of guides for research and support staff involved in natural resources projects. The general subject-matter here is the Design and Analysis of Experiments.

Other guides give information on allied topics. Your comments on any aspect of the guides would be welcomed.

1. Introducing GENANOVA

2. The Analysis of Variance

3. Contrasts

4. Orthogonality

5. Confounding

6. The Analysis of Covariance

7. Bivariate Analysis

This material was first produced as the statistical background to accompany a set of computer programs (collectively called GENANOVA) for the analysis of experimental data. We have reproduced the guide because it provides a very clear explanation of many important concepts concerned with the design and analysis of experiments. These concepts are described in a way that should be clear to non-statisticians and are equally relevant, whatever software is used for the analysis.

GENANOVA

Three computer programs, called GENVAR, GENCOV and GENBIV, comprised the original GENANOVA system as produced and marketed by the Applied Statistics Research Unit (asru) of the University of Kent. The programs were also adapted to be used from within the statistics package INSTAT, produced by the Statistical Services Centre. Since 1994 INSTAT - without GENANOVA - has been available for free distribution. We are very grateful that Professor Pearce and asru have given permission both to adapt this manual and to add the GENANOVA computer program to Instat for Windows, which is currently (January 2000) under development.

Section 1 provides the general context in which GENANOVA may be useful.

Section 2 reviews many of the important ideas of the Analysis of Variance.

Section 3 describes how contrasts are used to assess particular treatment effects and includes a brief explanation of why multiple comparison tests should be avoided.

An important feature of the associated computer programs is that they can be used for any blocked design, whether balanced or not. Section 4 considers what happens when the design is not "regular" or when practical problems have complicated the analysis of a simple design. An example used is of an experiment with 4 treatments in 3 blocks, in which the blocks, for sound practical reasons, are of sizes 13, 7 and 4.

Many books and computer programs emphasise the importance of using contrasts to assess treatment effects, and describe the methods, as in Section 3, when the experimental design is straightforward. The description in Section 5 is on the subject of confounding, which can arise when a design is non-orthogonal, and on how contrasts can still be estimated and interpreted.

Section 6 describes the under-used subject of covariance and considers, in particular how the use of covariates relates to blocking.

Section 7 describes how two variables can be analysed together in what is called a "bivariate analysis of variance".

---

2. The Analysis of Variance

2.1 General description

2.2 Nomenclature

2.3 The idea of significance

2.4 Estimation

2.5 What GENANOVA provides

2.1 ANOVA - General description

The analysis of variance can be thought of - at least in its original form - as a way of resolving differences of opinion. Perhaps there is open dispute, but more probably there is genuine questioning among a group of colleagues or even just doubts in the mind of one person. Whatever it is, someone has set up a hypothesis and people want to know if it accords with the facts. For example, there is a new preparation on the market and there are doubts whether it will work as well as the distributors claim. The hypothesis is always the point of view of the sceptics. They say that it has no effect, which is at least a definite and forthright statement that can be tested. (The opposite view - that there must be an effect of some sort but no one can put a figure to it - may well be the more reasonable, but it is too vague for anyone to test. On the other hand, if the hypothesis is discredited, it becomes the only alternative.)

A digression

At this point it may be helpful to recall how variability can be measured. Suppose that there are five values:

14, 16, 13, 15, 17

There are several ways and all have their uses, but the commonest and the one adopted in the analysis of variance is to calculate the variance and its attendant degrees of freedom. First of all, if the figures did not differ, what common value would be expected? The answer is their mean, which is 15. Consequently the deviations from expectation are:

-1, +1, -2, 0, +2

Naturally their sum is zero, but the method is to work with the squares of the deviations, not the deviations themselves, i.e. with 1, 1, 4, 0, 4. Their sum is 10. At first sight there are five quantities that can vary, but really there are only four. That is because of the constraint on the deviations to sum to zero; if any four of them are known, the other can be found from them, i.e. only four are free, the other is constrained. That being so, there are four degrees of freedom and the variance (or mean square) is 10/4, which equals 2.5.

Resumption

To return to the difference of opinion about the preparation. This is supposed to improve the growth of pot plants, so the team decide to take 12 pots, each with one plant, and to apply the substance to six of them, chosen at random, but not to apply it to the other six. After a while the total areas of leaves are measured on all 12 plants, with the following result:

With the substance 42, 50, 38, 51, 48, 47, Total 276

Without it 44, 48, 39, 36, 40, 45, Total 252

The two sides must now consider their respective positions. First, there are the sceptics who regard the 12 data as comparable. To them the expectation of all values is 44, i.e. the general mean or (276 + 252)/12, so they consider the deviations to be:

-2, +6, -6, +7, +4, +3

0, +4, -5, -8, -4, +1

giving a sum of squares of 272 with 11 degrees of freedom. Next there are the believers, who think that the two groups of six are different. To them the data in the first set have each an expectation of 46 (=276/6), giving deviations of:

-4, +4, -8, +5, +2, +1

and a sum of squares of 126 with 5 degrees of freedom. The other data have each an expectation of 42 (=252/16), giving deviations of

+2, +6, -3, -6, -2, +3

The resulting sum of squares is 98, also with 5 degrees of freedom. In all the sum of squares comes to 224 with 10 degrees of freedom. That is a reduction compared with the less flexible approach, because the use of two means instead of one necessarily allows of a better fit to the data.

The question is this: Does the reduction in the number of degrees of freedom explain the reduction in the sum of squares? The method is to take the difference between the two results. The sum of squares is 48 (= 272-224) with 1 (= 11-10) degree of freedom. If the hypothesis is true, i.e., the preparation has no effect, both parties should obtain the same variance, at least within sampling limits. If, on the other hand, it is not true and the preparation does have an effect, all the difference will have been concentrated on the additional line and it will give a greatly enhanced variance as a result. At this stage the analysis of variance can be written down. It goes like this:

Source	d.f.	s.s.	m.s.	F.
Due to preparation	1	48	48.0	2.14
"Error"	10	224	22.4
Stratum Total	11	272

The above table is typical. There are two lines derived from the two points of view and a third that represents the difference between them. For purposes of testing the important value is F, the ratio of two mean squares, i.e. 48.0/22.4 = 2.14. If the preparation had had no effect, F would be expected to equal 1.00, but not exactly so because of the variability and the allocation of treatments at random. How far can it differ from 1.00 before it needs to be taken seriously? Here tables will help. For 1 and 10 degrees of freedom, a value as high as 1.49 would arise by chance on about one occasion in four (P = 0.25). It could be as high as 3.28 on about one occasion in ten (P = 0.10), again purely be chance. The sceptics are entitled to say that the experiment has not proved anything; the difference between the two lots of plants could easily have been a matter of luck, a result of the random allocation having given a better set of plants to the new preparation. The believers can reply that there is evidence of the effect they expected and with more data the efficacy of the preparation could still be established. Both sides are right. There could be an effect, but it is insufficiently established by the data at present available.

2.2 Nomenclature

Before going further it will help to clarify the nomenclature. First of all, the experimental material is regarded as composed of units, each of which can be treated separately. In an agricultural context the units would be plots, in a medical they would be patients, in an industrial a group of similar components and so on.

It is not, of course, implied that there will be as many treatments as there are units. Indeed, it is usual for each treatment to be applied to several units. The number is called the treatment replication.

As has been explained, GENANOVA is intended primarily for the case when blocks have been formed, each block made up of units that are similar and therefore comparable. Again to repeat what has already been said, if that precaution is unnecessary or impossible and all units are compared one with another, there is a single block.

Then each unit is measured. As a result of that it acquires a datum. In ordinary contexts the plural is the familiar data, but in the specialised sense of a set of data for analysis and study, one from each unit, the word is variate.

The sum of squares with the fewer degrees of freedom is traditionally ascribed to experimental "error". It represents variation that cannot be explained by any source of variation considered in the design. Some people dislike the term. It is used here with inverted commas out of deference to the objectors and not for any other reason. The sum of squares with more degrees of freedom is that for the stratum total. In general, treatments are compared by applying them to different units within blocks. The stratum is of units within blocks, the one for which GENANOVA is intended. The sum of squares represents the total variation to be found in the stratum.

The deviations found by the sceptics are of special importance and have a special name, being known as the residuals. The sum of their squares is going to be used in several contexts as a measure of the uncontrolled variability or error, but it is all very well to quote a figure for the experiment as a whole. A research worker will want to know where the error came from, i.e. which units gave the aberrant results. If the results are more variable than expected an examination of the residuals may reveal the cause. Perhaps large values are found whenever the pump in the corner is switched on and causing vibration. Perhaps they mostly occur when Alan is making the measurements or when the weather is hot. Clues of that kind can be invaluable for avoiding similar variability in the future.

The error mean square is commonly called the error variance or just the variance. Although it provides a valuable measure of variability, it is often better to use its square root, which quantity is known as the standard error of an observation (or datum). One advantage lies in its restoring the original scale of measurement. If the original data are in grams, the variance is in grams squared and that is difficult to visualise, but the standard error is in the same unit as the data themselves. Hence it is more easily understood.

Sometimes a set of data, one from each unit, is introduced not on its own account but in the hope that it will shed light on the variate, i.e. on the quantities being studied. For example, the ability of a child at the end of a teaching experiment must depend to a large extent upon its ability at the start and a lot might be gained by measuring initial skill in order to make allowance for it at the end. The set of data so obtained, one from each unit, is called a covariate. It is not a variate because no one is asking about it; it is only an aid to the study of something else.

The form of analysis can sometimes be simplified by allowing for artificial covariates introduced for mathematical reasons. (Examples will be given in Section 6.4.) Such covariates are called either pseudovariates or dummy variables. Some people use one name and some the other.

2.3 The idea of significance

The value of P is called the significance level. How small must it be before the effect is established? The answer will not be the same for everyone; it depends upon the prior beliefs of those involved. Someone who was already nearly convinced might need little further evidence. On the other hand, someone who thought that there was strong evidence on the other side might require an exceedingly low value of P before giving in. There is the instructive story of an experimenter with a guilty secret. He had forgotten to apply the treatments. When P turned out to be less than 0.01, he astonished everyone by refusing to believe that they had had any effect. At last he confessed. The story serves as a reminder that P will fall below 0.01 on one occasion in a hundred even when the treatments are ineffective. In an absolute sense a low significance level does not prove anything though it may afford a strong argument.

Since the report of an experiment will probably be read by people with a wide range of initial beliefs, there is no one level of P that will apply to all. By convention if the value is more than 0.05 many editors of journals will refuse to publish the conclusion at all. That is a pity because suggestions can be useful, especially those that set up a train of thought. (Admittedly it is up to the original writers to do the additional work needed to clear up important ambiguities in their own work, but other people may have different priorities and different interests.)

Also, whatever historical reasons there may have been for its adoption, the value of 0.05 is arbitrary. Even if there were agreement on the significance level to be used, differences between means cannot be classified into those that are "significant" and therefore important and those that are "non-significant" and therefore to be ignored because the actual size of the difference matters as well. A non-significant result may be quite large. If so, it will be important if it can later be confirmed. On the other hand, if a difference is too small to be important, there is no need to bother whether it is significant or not.

2.4 Estimation

Although the analysis of variance was devised in the first place for significance testing it has another and more useful purpose. In Section 2.1 there were those who thought that the preparation must do something to the leaf area but they did not know by how much. Their attitude could have been quite reasonable. Further, if a significance test does show that the treatments have had an effect, this leads to another question. How large is it?

A block experiment is comparative. That is to say, it does not set out to find values for individual treatments but only for differences between them. To take the pot plants as an example, those untreated gave a mean leaf area of 42 and those treated gave 46. It would be unwise to expect another lot of plants to give the same figures; they could be older or grown in different surroundings, but the difference, namely 4, might very well apply to the second lot, at least as an approximation.

How well is the figure of 4 known? It needs to be complemented by its standard error, which is found by taking the error mean square and multiplying it by a quantity that is here represented by the Greek letter theta, written . In GENANOVA that multiplier is given by the algorithm. The standard error is the square root of the variance. In this instance the error mean square is given by the analysis of variance as 22.4 and there is no difficulty about . For a completely randomised design in which one treatment has p data and the other q,

= 1/p + 1/q.

Here, where both treatments have 6 data, so equals (1/6 + 1/6) = 1/3. Hence the standard error of the difference is the square root of 22.4/3 or 2.73. Many statisticians would think that enough. They would be content to report that the effect of applying the preparation was +4.0 with a standard error of 2.73, leaving the rest to the reader.

Others would prefer to give what are known as confidence limits. They would refer to tables to find the quantity called t. It has to be looked up for a probability level - again 0.05 is usual - and the error degrees of freedom. For P = 0.05 and 10 d.f. it is 2.23. Multiplied by the standard error, it gives 6.09. Hence the value of the effect lies between -2.09 (= 4.0 - 6.09) and 8.09 (=4.0 + 6.09) with one chance in twenty (P = 0.05) of those limits being exceeded.

For purposes of computation, testing and estimating are closely related. Indeed, the example of estimation just given has also been an example of testing. If zero lies between the confidence limits, it is a possible value for the effect, i.e. perhaps no effect exists. Nevertheless, in spirit the two are far apart, while in practice humble estimation is often more valuable than esteemed testing.

2.5 What GENANOVA provides

Genanova gives residuals. It is important to have them. If everything has gone well, there may be no need to examine them. On the other hand, if the error variance is unexpectedly high, they may be needed to suggest what went wrong. Genanova also gives the analysis of variance in the form set out in Section 2.1 and also the treatment means, possibly after adjustment if that has been needed. (See Sections 4.2, 6.2 and 7.3.) Where relevant, other matters will be reported as well.

The user is given the opportunity of indicating any treatment contrasts of special interest. (A contrast is a more general form of the differences used here. It will be explained more fully in Section 3.) The program will then estimate the value and the standard error of each contrast about which enquiry has been made.

The analysis of variance will always be given in the form used in Section 2. Where blocks are used, some people will expect a further line to show the degrees of freedom and sum of squares for block differences, but nowadays that is seen as a survival from the past. When the subject started, the analysis of variance was a study of the complete deviations, i.e. the differences of data from their general mean, but these days the introduction of blocks is regarded as splitting each such deviation into two parts. First, there is the difference between the datum and the block mean and then there is the difference between the block mean and the general mean. That is expressed by saying that there are two strata:

1. that of units within blocks,

2. that of blocks within the whole.

The intervention of treatments has taken place within the first stratum and only its analysis will be considered here. The line usually attributed to blocks is really the stratum total for the blocks within the whole and that is not under study.

[TOP]

---

3. Contrasts

3.1 The case of several treatments

3.2 Interactions

3.3 Higher order interactions

3.4 Multiple comparisons

3.5 GENANOVA and contrasts

3.6 The treatment sums of squares

3.7 Some useful contrasts

3.1 The case of several treatments

The example in Section 2.1 had only two treatments. Consequently there is only one question that can be asked about them in testing (Do they differ?) and one in estimation (By how much do they differ?). The situation becomes more difficult when there are more. Suppose, for example, that there are three, blandly called A, B and C. Unless someone can say what treatments the letters represent and unless there is an explanation why they were chosen, there is no way of knowing how to proceed. The data analyst is being asked to answer an undefined question.

The difficulty really arises from there being two degrees of freedom for treatments, showing that two questions are being asked simultaneously. They have to be disentangled and answered separately.

In order to define the questions someone may reply that the three treatments are

[A] No application of fertiliser.

[B] Application of fertiliser at half the recommended rate.

[C] Application of fertiliser as recommended.

With that made clear the analyst can see how to proceed. The first question concerns the efficacy of the fertiliser as ordinarily used, i.e. the difference between C and A, written (-1, 0, +1). The second concerns the effect of a half application. Does it lie somewhere round the halfway point in response, or does it lie above or below that point? The next stage is to compare B with the mean of A and C, that being written as (-1/2, +1, -1/2).

Someone else may reply that his problem is quite different. In his experiment A is the existing standard and B and C are modifications that may well prove to be better. In that case his need is to compare B with A, which can be written (-1, +1, 0) and C with A, written (-1, 0, +1). If either of those contrasts proves to be significant, an advance will have been achieved. Other people conducting experiments with three treatments might join in. It is quite amazing how many various kinds of problem there can be.

The difficulty has become apparent. The F-test with two degrees of freedom for treatments may indeed suggest that there is something there, but what? Which pair of the degrees of freedom should be used? Further, there is a danger. One of the degrees of freedom may be significant (F being high) and the other not (F being low). The value of F when they are amalgamated will take some intermediate value, which may well be non-significant. In that case something important will be missed. (That danger is less when estimating.)

It will be noticed that the coefficients of a contrast always sum to zero. If GENANOVA asks for a contrast and is given coefficients that fail the test, the message

That is not a contrast

will be displayed and they will be ignored.

3.2 Interactions

With four treatments another kind of contrast makes its appearance in addition to those already considered. It could arise, for example, with the experimenter who had a standard, A, and two suggested improvements, B and C. Suppose that he wants to try B and C together. In this context it is usual to call the existing standard, (1), so the treatments are now

(1), B, C, BC.

Here B and C are called factors of the experiment. First of all, does B have an effect? That implies the contrast (-1, +1, -1, +1) which is known as the main effect of B, both levels of C being used in the assessment. Next, does C have an effect? That implies (-1, -1, +1, +1) the main effect of C. There is a degree of freedom still undetected and it arises from the possibility that B and C will, to use the technical term, interact. Will the effect of factor B be the same when C is not used, i.e. (-1, +1, 0, 0) as when it is, i.e. (0, 0, -1, +1) The difference is (+1, -1, -1, +1). (The same contrast will be reached by asking whether C has the same effect in the presence and absence of B.)

The interaction is of immense importance. It should always be examined first. If it exists, there is no point in enquiring about the effect of one factor averaged over the levels of the other. In that case a contrast like (-1, +1, -1, +1) has no useful meaning. Instead, the particular effects, (1, +1, 0, 0) and (0, 0, +1, +1) have to be looked at separately and the same goes for the main effect of C, (-1, -1, +1, +1), which needs to be replaced by (0, -1, 0, +1) and (-1, 0, +1, 0). Estimation has to take place separately in the presence and absence of B.

There is no difficulty in writing down the contrast for an interaction; it can always be found by multiplying corresponding coefficients of the two interacting effects. Thus, in the example, the interaction of:

	-1	+1	-1	+1
and	-1	-1	+1	+1
proved to be	+1	-1	-1	+1

which illustrates the rule, because +1 = (-1 * -1), -1 = (+1 * -1) and so on. To take a further example, the enquirer who was studying the effect of fertiliser on pot plants might well have wondered whether the size of pot came into it. To find out, six treatments would be needed, namely,

0L

1/2L

1L

0S

1/2S

1S

where L and S indicate large and small pots, while 0, 1/2 and 1 indicate the amount of fertiliser. For fertiliser there are the two contrasts already noted, known usually as the linear and the quadratic, i.e.

L	(-1	0	+1	-1	0	+1)
Q	(+1/2	-1	+1/2	+1/2	-1	+1/2)

They have been taken over both sizes of pot. There is also, P, the size of pot taken over all fertilisers, represented by

P

(+1

+1

+1

-1

-1

-1)

The interactions are:

LxP	(-1	0	+1	+1	0	-1)
QxP	(+1/2	-1	+1/2	-1/2	+1	-1/2)

which make up the fourth and fifth degrees of freedom between the six treatments.

In data analysis the first task is to look at the interactions. If either L×P or Q×P exists, there can be no unqualified statement about the effect of plot size because it depends upon the amount of fertiliser supplied. Equally, if L×P is significant, there can be no unqualified conclusion about the size of the linear effect, L, because it depends upon the sort of pot, and similarly with Q×P.

Some reservations were expressed earlier about the custom of always testing and rarely estimating, but they apply with much less force to interactions. If there are two factors and if differences between treatments are large enough to require assessment, anyone who reports the outcome has to decide whether or not to qualify general statements about the factors. It is then that the significance levels of interactions become important. As ever, common sense must prevail. Some interactions are almost certain to exist while others may be scarcely conceivable, but there are many where some guide is needed whether to accept them or not. If arbitrary decisions are to be avoided, the significance levels can help.

3.3 Higher order interactions

Where there are three or more factors, higher order interactions become possible. Perhaps A×B will depend upon the level of C. That comes to the same thing as saying that A×C depends upon the level of B or that B×C depends upon the level of A. It is written A×B×C and it is found by an obvious extension of the method used for two-factor interactions. The three main effects are written down and for each treatment the three corresponding coefficients are multiplied to give the coefficient for the interaction. Mostly three-factor interactions are difficult to describe when writing a report, but if marked they should not be disregarded.

In principle the process can continue indefinitely, but it takes a genius to describe an interaction with four or more factors. Also, it is more difficult to establish the significance of a two-factor interaction than a main effect, of an interaction with three factors than one with two and so on. Fortunately for experimenters who have to explain their conclusions to others, it is unusual for a four-factor or higher order interaction to prove significant.

3.4 Multiple comparisons

One common way of evading the difficulty of deciding on contrasts is the use of multiple comparisons. There are many such methods and they do not agree in the results they give, which is sufficient reason for being wary of them. What they do is to consider all possible elementary contrasts, i.e. those that involve only two treatments, and to note which are significant at a given level, bearing in mind there are a lot of such contrasts and overall the chances of finding something significant is thereby increased.

To explain further, if there are three treatments, A, B and C, there are three elementary contrasts, A versus B, A versus C and B versus C. Because there are three of them, if each has an independent chance of appearing significant on one occasion in twenty (P = 0.05), the chance of something being declared significant is nearer 0.15 than 0.05. (Actually they are not independent and that has to be taken into account as well.) The resulting test delights the mathematician by its elegance; it also delights the less thoughtful sort of experimenter because it appears to justify them in not bothering about objectives. In fact, the whole approach is mistaken.

It is wrong, first, because it misses the point.

1. Experimenters are not necessarily interested in testing. They want to estimate as well.

2. Contrasts of interest are not usually elementary. They may involve several treatments, e.g. those in the last section.

3. Such tests ignore the purpose of an experiment.

If the intention does involve the study of an elementary contrast, the conclusion should not depend upon the magnitude of other contrasts. Either they should be the object of a separate study or they are irrelevant to the purpose of the experiment and should not be allowed to influence its interpretation.

It is wrong also because it leads to nonsense. To take a simple example, following the usual practice of putting lower-case letters after means to show non-significant groups, the three treatments in the fertiliser experiments on pot plants might give the following result:

No fertiliser 40.1 a

Half application 42.6 ab

Full application 44.8 b

What does it mean? At least it is clear that the full application gives larger leaves than doing nothing because the extreme treatments have no letter in common, but what about the half application? It may be giving the same result as no fertiliser, both being in group a. If so, it must be different from the full application, but that cannot be because both treatments share the letter b. The obvious interpretation is being missed, namely that the fertiliser does give larger leaves, a half application having about half the effect of a full one. Use of the contrasts (-1, 0, +1) and (+1/2, -1, +1/2) would have made the situation completely clear. For the reasons given, multiple comparisons are to be strenuously avoided.

3.5 GENANOVA and contrasts

It is a special feature of GENANOVA that the user has complete freedom in specifying the contrasts to be studied. Some will not welcome the responsibility, preferring to enter the data and then leave it to the program to decide what comes out, but good experiments are not conducted like that. They exist to obtain answers to questions and the questions must be specified. The statistical way of doing that is to state a contrast, whether for estimation or testing the context must decide. Once the skill of selecting contrasts has been acquired, it deepens and extends understanding of the analysis of variance.

In GENANOVA contrasts are usually entered as integers. For example, (+1/2, -1, +1/2) becomes (+1, -2, +1). Similarly (+1, -1/3, -1/3, -1/3) becomes (+3, -1, -1, -1). That is not done for any deep mathematical reason but to achieve a neat form of output. Also, the convention is one that is well established. Without it, one person might be talking about the contrast (+1/2, -1, +1/2) and another about (-2, +4, -2) without their seeing at once that they are talking about the same thing. In estimation, scaling is important but there need be no difficulty. If the user wants to know about (+1/2, -1, +1/2) and the output gives results for (+1, -2, +1), it is sufficient to divide both the value of the contrast and the standard error by 2.0. Its contribution to the treatment sum of squares, its F-value and its efficiency factor will not be affected.

For each specified contrast GENANOVA gives the value of the contrast and its standard error. It gives also the component of the treatment sum of squares corresponding to the contrast and the consequent F-value. There is other information as well, but that will be explained later.

3.6 The treatment sums of squares

Where the individual contracts need to be considered - and that is nearly always - the treatment sum of squares is not usually presented as a whole but in several lines. Thus, with a factorial treatment structure, one factor having three levels and the other two, instead of a single line with five degrees of freedom for treatments, there would be three lines, one with two d.f. for the first factor, another with one d.f. for the second and the last with two d.f. for the interaction. That is good practice and GENANOVA provides for it. (Indeed, it encourages the user to go further and break down the treatment sum of squares into a separate component for each degree of freedom and not just for groups of them. Thus, in the above example, if the factor with three levels represented three levels of application, the user is able to break down the two degrees of freedom into one for the linear effect and one for the quadratic.)

At this point a difficulty appears that was really there all the time. Introductory texts to the analysis of variance can give the impression that the components necessarily add up correctly to the value given in the analysis of variance. In fact, though that usually happens in simple cases, there is no general rule to that effect. Users of programs like those in GENANOVA, which deal with faulty data and designs that are less than ideal, may quickly discover exceptions. If any are found, there is no need to worry. The components add up correctly only if they are estimated completely independently of one another and that is not always possible to arrange. In the analysis of variance, they will often do so; in the analysis of covariance and in bivariate analysis such an outcome is unusual.

3.7 Some useful contrasts

Once users get the idea, they usually find little difficulty in writing down the contrasts they need, but it may help to give a few examples. First, when there are only three equally spaced levels, as in Section 3. 1, the usual contrasts are (-1, 0, +1) and (+1, -2, +1). As has been seen, the first measures the general slope while the second measures any curvature in the response.

If there are four equally spaced levels, the usual contrasts are (-3, -1, +1, +3), (+1, -1, -1, +1) and (-1, +3, -3, +1). The first (the linear effect) measures the general slope and the second (the quadratic effect) the curvature, while the third (the cubic effect) measures a tendency to inflect, i.e., to curve first in one direction and then in the other as with a sigmoidal response curve. (In fact it is more usually taken simply as indicating some sort of departure from a second-degree curve.) Sometimes, despite the objections of the statisticians, experimenters use levels like 0, 1, 2, 4, or doses proportional to those figures. They do not represent any regular series but, if they are used, the appropriate contrasts are (-7, -3, +1, +9), (+7, -4, -8, +5) and (+3, -8, +6, -1), corresponding respectively to the contrasts given for equal spacing of doses.

Although experiments are sometimes designed with five or more levels, the reason is not usually to determine the parameters of higher-order curves. Mostly so large a number of points is introduced to detect some special feature, such as an abrupt change of slope or other discontinuity. Nevertheless there are times when it could be helpful to know the linear and quadratic effects. (It will be assumed that equally-spaced levels are used.) If there are five, the linear and quadratic effects are given respectively by (-2, -1, 0, +1, +2) and (+2, -1, -2, -1, +2); if there are six, the corresponding contrasts are respectively (-5, -3, -1, +1, +3, +5) and (+5, -1, -4, -4, -1, +5). Any residue of the treatment sum of squares left over after the exclusion of the linear and quadratic effects should be attributed to departures from a second-degree curve. An F-test on the residue investigates the adequacy of such a curve in representing the response to increasing doses, though strictly speaking it will be exact only if the components add up correctly. (See the last section.)

Interactions have already been considered; their contrasts are found by multiplication using the method in Section 3.3.

A difficulty sometimes arises when the levels of a factor are qualitative and there is no reasonable way of expressing them on a quantitative basis. For example, they might represent the use of several unrelated substances. If that is so, there is no reason to choose one set of contrasts rather than another, apart from the requirement that there must be a reasonable expectation that all members of the set will be estimated independently. Usually it is simplest to add treatments one at a time, i.e.

(+1, -1, 0) and (+1, +1, -2) for three levels,

(+1, -1, 0, 0), (+1, +1, -2, 0) and (+1, +1, +1, -3) for four levels and so on.

The chosen contrasts are then presented to the program one by one, their sums of squares being added to provide an F-test. In this instance also there could be some imprecision on account of the contrasts not being independent, but it is unlikely to be large.

An important special case arises with the so-called quality-quantity interaction. To take a simple example, suppose that two substances, A and B, have been applied at levels 0, 1 and 2. Since A0 is the same as B0, there are only five treatments, not six; they will be taken in the order, 0, A1, B1, A2, B2. It is advisable to give double replication to 0, i.e. to regard it as an amalgamation of A0 and B0, which indeed it is. The main effect of substances does not involve 0, its contrast being (0, +1, -1, +1, -1). The linear effect for dosage is given by the contrast (-2, 0, 0, +1, +1) and the quadratic by (+2, -2, -2, +1, +1), leaving (0, +1, -1, -1, +1) for the interaction. (Again 0 is not needed.) Extension to larger treatment sets is not difficult.

[TOP]

---

4. Orthogonality

4.1 Introduction to Orthogonality

4.2 Design assessment

4.3 Adjusted treatment means

4.4 The uses of non-orthogonality

4.1 Introduction to Orthogonality

Most designs have a high degree of regularity and that is a good thing. Nevertheless when practical difficulties have stood in the way or when there has been damage, the regularity may be lost. It is then that a set of programs, like those in GENANOVA, prove especially useful.

The most sought-after form of regularity is orthogonality. It arises whenever each block is made up in the same way. To take an example, most experimenters with 12 units and 4 treatments (A, B, C and D) would think first of the design known as randomised complete blocks, which is the most commonly used of all designs. In this instance it would go like this:

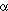
Design	Block I	A	B	C	D
	Block II	A	B	C	D
	Block III	A	B	C	D

That is very simple and greatly to be commended if it fits the problem.

IMPORTANT NOTE. Here and throughout it will be understood that after a set of treatments has been allocated to a block, the further allocation of individual treatments to units must be at random.

It is orthogonal because each block is made up in the same way, i.e. each contains each treatment once. However, orthogonality goes further than that. There is, for example, no need for all treatments to be equally replicated and sometimes it is better if they are not. Indeed, if the task is to compare new treatments, A, B, C and D, with an existing standard, O, there is a lot to be said for duplicating the standard. It might be wise to design the experiment thus:

Block I	O	O	A	B	C	D
Block II	O	O	A	B	C	D
Block III	O	O	A	B	C	D

Again the design is orthogonal because each block is made up in the same way. The matter can be taken further. A design like

Block I	A	B	C	D	E
Block II	A	A	B	B	C	C	D	D	E	E

also is orthogonal because one-fifth of each block is assigned to each treatment. That is to say, it is the proportion of the block occupied by each treatment that matters, not the number of units. (There is an implicit assumption that the block with ten units will be no more variable than the one with five, but that could well hold.)

What then are the advantages of orthogonality? First, simplicity, but also precision relative to the number of units. That can be shown by taking a design that is clearly non-orthogonal. Design 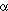requires blocks of four units, but they might not be available. Perhaps the only reasonable blocks contain three units each, so what is to be done? One solution is to use a design in balanced incomplete blocks as follows:

Design ß	Block I	B	C	D
	Block II	A	C	D
	Block III	A	B	D
	Block IV	A	B	C

In Design ß, treatment A has been omitted from Block I, B from Block II, C from Block III and D from Block IV, thus preserving balance between the treatments. What has been lost is precision. If someone wants to compare A and B, Blocks III and IV each give a direct comparison. That is not so for Blocks I and II. It is true that they do provide some information about the difference between A and B, because in Block I the mean effect of C and D can be compared with that of A and in Block II with that of B, but an indirect comparison is not as good as one that is direct. In Design 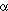on the other hand, each block gave a direct comparison, making three in all.

The situation is this: given any contrast and any design able to estimate it, there is a quantity (represented by the Greek letter, , called theta) such that the variance of estimation of the contrast using the design is × (error mean square). For a completely randomised design can be worked out from the replications, as was done for a difference of means in Section 2.4. If blocks are inserted and the resulting design is orthogonal, is unchanged. Hence, any reduction in the error mean square is passed to the variance of estimation of the contrast. If, however, the resulting design is non-orthogonal, may be increased. Unless any increase in is compensated by a comparable reduction in the error mean square, on balance the variance of estimation of the contrast will have been increased.

Designs 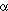and ß illustrate the point. For 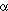and the difference between the means of A and B, it can be shown that equals 2/3, as would be the case with a completely randomised design. For ß it is 3/4. The ratio, 8/9, is known as the efficiency factor. Unless Design ß is going to give an error mean square less than 8/9 times that given by Design 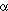, it would be better to use the latter.

If the efficiency factor equals one exactly, the design is said to be "fully efficient" for the estimation of the contrast being considered. An orthogonal design is fully efficient whatever the contrast.

4.2 Design assessment

Genanova contains a useful facility for assessing a suggested design. Whenever enquiry is made about a contrast it concludes its report by giving the values of (theta) and the efficiency factor. (Of course, the program will require data if it is to run but the choice is immaterial. Usually it is simplest to make the first datum equal to 1 and the rest to 0. Such "data" do not really lend themselves to the analysis of variance, but the only values needed from the output concern design characteristics.)

It will be instructive to assess the design proposed in Section 1.2, namely:

Design ¢

Block I

A

A

A

B

B

B

C

C

C

D

D

D

D

Block II

A

A

B

B

C

C

D

Block III

A

B

C

D

This will be compared with the orthogonal design that resembles it most closely and one that the investigator might have preferred to use had it been possible, namely:

Design ð

Block I

A

A

A

B

B

B

C

C

C

D

D

D

Block II

A

A

B

B

C

C

D

D

Block III

A

B

C

D

Because Design ð is orthogonal, it will be fully efficient for all contrasts, i.e. it will always give the same value of as would be obtained from a completely randomised design with the same treatment replications. Accordingly, when seeking efficiency factors for Design ¢, it will be enough to compare its value of with that given by Design ð.

In comparing designs a lot depends upon the contrasts to be studied. A design may be ideal for one set but ineffective for another. Here two possibilities will be considered. First it will be supposed that A, B, C and D are factorial, i.e. they represent respectively (1), X, Y, XY. That being so, the contrasts of interest are

(+1, -1, +1, -1), (+1, +1, -1, -1), (+1, -1, -1, +1)

Next it will be assumed that each treatment, B, C and D, represents an addition to the one before, the basic treatment being A. In that case the desirable contrasts are

(-1, +1, 0, 0), (-1, -1, +2, 0), (-1, -1, -1, +3)

Of course, in both cases modifications may be needed in the light of the data. With the first set, a large interaction might call for examination of particular effects; with the second, if the additive included at C showed an improvement on A and B, the last contrast might well need reconsideration.

By considering first the factorial set of treatments, when Design ð is used, it will be found that equals 0.6667 for all contrasts. Using Design ¢ it is again the same for all three contrasts, this time being equal to 0.6729, giving an efficiency factor of 0.9908 (=0.6667/0.6729) for all three contrasts. That is to say, the loss of information due to the non-orthogonality has been evenly spread and amounts to about 1% whatever the contrast, i.e. very little has been lost as a consequence of the choice of design. On the other hand, the error mean square, which is the other component of precision, could have been appreciably reduced by the use of a realistic blocking system.

To turn to the other set of contrasts, for Design ð their values of are respectively 0.3333, 1.0000 and 2.000. For Design ¢ they are 0.3333, 1.0000 and 2.0565, giving efficiency factors of 1.0000, 1.0000 and 0.9725. In this instance all the loss has fallen on the last contrast, but in total it has been about the same as with the other set.

4.3 Adjusted treatment means

With non-orthogonality the treatment means have to be adjusted to allow for the blocks in which the treatment occurred. A straightforward mean of data from any treatment will be biased according to whether it found itself in good blocks or not. For example, suppose that Treatment A did not occur in Block I but the performance of the other treatments in that block was better than elsewhere. Clearly A has been handicapped by its omission from a good block and an upward adjustment is needed on that account. Equally, if Block I had in general given poor results, A will have gained by missing it and its mean should be reduced. Similarly, if a treatment is over represented in a block, adjustment is necessary but in the opposite direction from that needed to repair an omission. The aim is to obtain means that indicate without bias what the treatment would have done if it had been applied to all the units of the experiment and not just to some of them.

These adjustments provide an alternative approach to the concepts of and efficiency. Like all other quantities derived from data, the adjustments are estimated figures and each has its own standard error. With a non-orthogonal design, where they have to be introduced, that adds to the overall standard error of an adjusted mean. With one that is orthogonal or one that is completely randomised, they are not needed and consequently they do not increase the value of .

One consequence of the adjustments can puzzle those not used to them. An experiment has been conducted and means have been worked out for each treatment. Then an analysis of variance is carried out and different values are found. That is quite correct because the adjustments have been applied. What can be more puzzling, however, is the realisation that different algorithms may give different means. Here it may be recalled that block experiments are only comparative. An experimenter does not take a random sample of all possible units in the world but only those available. Even then there could be selection to obtain uniform blocks, some units being discarded because there are no others like them. In these circumstances the experiment does not estimate means but only contrasts between them. If the experiment had been conducted in a different hospital or in a different factory or in a different school or on the other side of the hill, the means might well have been different. Given generally similar conditions, however, it is to be expected that good treatments here will be good treatments there, i.e. the values of contrasts will have remained about the same.

One consequence is that the general level of means is not fixed. If there are three treatments, respective means of 14, 19, 15 give the same contrasts as 15, 20, 16. Strictly speaking one solution is as good as another, though in practice people want some sound indication of the level. The algorithm used in GENANOVA secures that the mean of the means equals the general mean of the data presented, no regard being paid to the number of data for each treatment.

4.4 The uses of non-orthogonality

Mostly the inexperienced are fearful of non-orthogonality. Perhaps they are not confident of their ability to carry out the necessary analyses of variance; perhaps they have been told that it is "wrong". As far as difficulties with computing are concerned, it is precisely to overcome them that GENANOVA has been evolved. As to its being wrong, admittedly non-orthogonality must lead to efficiency loss, but that must be seen in relation to the error mean square. If a better blocking system will reduce variability within blocks, on balance there could be an advantage. Also, with a little ingenuity it may be possible to concentrate the efficiency loss on contrasts of little interest and here GENANOVA can help by assessing the designs that may be proposed. In any case, if a really awkward blocking system has been imposed by practicalities or if an experiment has suffered from mistakes or accidents, there may be no alternative to the acceptance of non-orthogonality.

[TOP]

---

5. Confounding

5.1 Introduction to Confounding

5.2 Consequences of confounding

5.1 Introduction to Confounding

Sometimes there are contrasts among the treatments, like high-order interactions, that can be discounted. Someone who was exploring a range of factors might easily have eight treatments, made up of three factors, each at two levels, thus:

(1), X, Y, XY, Z, XZ, YZ, XYZ.

(Note that the factors are introduced one by one to give the standard order of such a set of treatments.) Clearly the investigator needs the main effects and also the two-factor interactions to see which factors have to be studied in conjunction. It would perhaps be helpful to know about the three-factor interaction, i.e. X×Y×Z as well. There could, however, be difficulty in finding blocks large enough to contain eight units, bearing in mind that each should as far as possible be uniform in itself. It is in such circumstances that the device of confounding comes in useful.

The method is more easily explained if all the contrasts are stated explicitly. First there are the main effects:

X	(-1	+1	-1	+1	-1	+1	-1	+1)
Y	(-1	-1	+1	+1	-1	-1	+1	+1)
Z	(-1	-1	-1	-1	+1	+1	+1	+1)

Incidentally, the patterns among the coefficients show the value of using the standard order of treatments. The next necessary contrasts are those that arise from the two-factor interactions, found in the usual way by multiplying together the coefficients from the contrasts of the associated main effects. They are:

Y×Z	(+1	+1	-1	-1	-1	-1	+1	+1)
X×Z	(+1	-1	+1	-1	-1	+1	-1	+1)
X×Y	(+1	-1	-1	+1	+1	-1	-1	+1)

A standard order has been obtained by omitting the factors X, Y and Z in turn. All the above contrasts are essential. There remains only the one that can be sacrificed if necessary, namely:

X×Y×Z

(-1

+1

+1

-1

+1

-1

-1

+1)

If blocks of four units are taken, half receiving (1), XY, XZ and YZ, and half X, Y, Z and XYZ, the three-factor interaction will have been lost. Anyone who tried to work it out would soon discover that no treatments with a positive coefficient ever occurred in the same block as one with a coefficient that was negative. Consequently the two groups cannot be compared with one another, at least not by using units within a block. (It could be done by comparing whole blocks, but that involves a different stratum) Put another way, in the stratum of units within blocks, which is the one studied by GENANOVA, the analysis of variance has nothing to say about the confounded contrast; the efficiency factor is zero. Nevertheless there has been an advantage. Although the contrast in which there is little interest has been lost, the others are known more precisely than they would have been using blocks of eight units. Such blocks would have been difficult to find and variable if found, but those with four units should give a smaller error mean square. Either way the contrasts of interest are estimated with full efficiency.

5.2 Consequences of confounding

When a contrast is confounded the formally correct way to answer an enquiry about its value is to say that it is unknown. In fact, it has been confounded because its value is believed to be negligible; hence, the algorithm assigns it a value of zero with zero standard deviation. One consequence is that GENANOVA, in company with some other programs, adjusts the treatment means to make the value of any confounded contrast equal to zero, while leaving other contrasts unchanged in value. Some people find the alteration disconcerting. They work out the mean of a treatment from the data and assume it to be correct, but the output makes it something else. Actually the change is quite logical. If the contrast has in fact been confounded because it is assumed to be too small to matter, then any difference between the group of blocks that had treatments with positive coefficients and those that had negative ones, must arise from differences between the blocks and not differences between the two groups of treatments. What the adjustment has done has been to refer each treatment mean to the blocks as a whole and not just those in which the treatment occurred. It is therefore an improvement.

The confounding of a contrast can lead to other contrasts being lost. To take the design described above, someone might want to compare the treatments, XY and X. Because they are in different groups there is no way of doing so. In such circumstances the output will report that the contrast cannot be estimated, so no one will be misled. In practice the difficulty is not very important, but it needs to be borne in mind. (Actually, if anyone wanted to know whether Y had an effect in the presence of X and was prepared to disregard any possible effect of a three-factor interaction, the natural thing would be to compare XY and XYZ with X and XZ.)

In more complicated situations several contrasts may be confounded. GENANOVA always looks for confounding and reports anything it finds. It does so by seeking disconnected parts. Thus, in the design used for illustration, under Part 1 it would list the treatments, (1), YZ, XZ and XY together with the numbers of the blocks that contained them. It would report under Part 2 the other treatments and the other blocks. Finally it would give the message "All disconnected parts found". The facility is useful because an unwary user might not notice that someone had introduced confounding into the design. Also, when data are lost or the design has suffered an accident, confounding can creep in without anyone realising what has happened.

[TOP]

---

6. Analysis of covariance

6.1 Adjustments by covariance

6.2 Computing the analysis of covariance

6.3 Double covariance

6.4 Pseudovariates

6.1 Adjustments by covariance

In the analysis of covariance there are two variates. Besides y, which is the subject of study, there is x, known as the covariate, which cannot have been affected by the treatments and which is thought to be related to y. If that can be shown to be so and if the precise form of the relationship can be established, it should be possible to remove a source of variability in the 'error' in the y-data by adjusting them all to a standard value of x. Such an adjustment, if made, will not bias the treatment means of y because x cannot impart any effects of treatments. It can, however, remove 'error' related to its own chance variation.

To take some examples, a medical research worker may examine a group of patients at the start of an experiment and measure a number of characteristics on each. At intervals during the investigation the same measurements may be repeated to see if the treatments are having differential effects, but how are the initial records to be used? One possibility is to subtract the initial figures from those found later and to analyse the differences. That might in fact work very well, but what if the symptoms initially recorded could be expected to diminish (or intensify) over the course of time? The question then becomes: Given an initial value (x), what does that indicate about the value (y) to be expected at some later date? That is just the sort of question for which the analysis of covariance was developed.

Another example of its use arises when there are spatial trends. The top of an oven is commonly hotter than the bottom, but by how much? If treatments are applied to units in a random manner, some may be allocated to hotter locations than others, but a covariance adjustment on the height of each unit above the oven floor should reduce the variability introduced.

6.2 Computing the analysis of covariance

Computationally an analysis of covariance is more lengthy than an ordinary analysis of variance besides involving more concepts. Despite that, it is not as difficult as some people seem to imagine. GENANOVA proceeds in this manner: First it finds the residuals of x and adds their squares to find the error mean square, Exx, of the analysis of variance. It then repeats the calculations to find Eyy. What it does next is to multiply together corresponding residuals and to add the products, one for each unit, to find Exy. Then, if the relationship between x and y can be represented reasonably well by a straight line, the slope of that line will be Exy/Exx (= b, the so-called regression coefficient). That is to say, if x lies above its mean value by an amount, d, then y can be expected to lie above its mean by b*d. (Of course, d can be negative, indicating an x-value below the mean. The regression coefficient also can be either positive or negative because, dependent on which quantities were being studied, an increase in x could imply either an increase or a decrease in y.)

It should be noted that the regression coefficient sums up the position for a given set of data and may not apply for another. There could be several ways in which a change in x could bring about a change in the expected value of y and the various mechanisms might lead to different regression coefficients. The calculation has found a value of b appropriate to one mixture of mechanisms. On another occasion it could be different. For example, the regression coefficient found from the stratum total line may be different from that found from the error line. If it is, the analysis of covariance could well make adjustments of some importance because clearly the treatments are not just emphasising effects already present in the error but are introducing fresh ones.

From now on, what happens is effectively this: All values of y are adjusted to a standard value of x and an ordinary analysis of variance is carried out on them. (At several places there are short cuts in the algorithm, in fact the adjusted data are never explicitly evaluated, but the intention is as described.)

To anyone studying the output, there is a reduction in the number of degrees of freedom for both error and stratum total. That is because it has been necessary to estimate the regression coefficient from the data. The most important difference, however, concerns the value of , the multiplier of the error mean square to give the variance of a contrast. In the analysis of covariance the contrast is worked out for y and then adjusted for the value of the contrast in x. If that happens to be 0, no adjustment is made, but if the randomisation had led to the contrast having an appreciable value in x, the adjustment would be made and would itself contribute to the variance. The former value of would increase to ^'. As a consequence the covariance adjustment must reduce the error mean square to less than /^' times its unadjusted value or the covariance adjustment will have led on balance to less precision, not more.

It is sometimes said that no harm can result from introducing a covariate, x, apart from the loss of a degree of freedom, but that is not so. If the randomisation distributes the values of x awkwardly over the units so that some contrast has a high value in x, ^' may be appreciably larger than and the covariance adjustment will have done harm unless there is a compensating reduction in the error mean square. In GENANOVA the value of /^', called the covariance efficiency, is always given. It corresponds to the efficiency factor of a non-orthogonal design. There is a difference, however. The experimenter knows from the start what the efficiency factor is going to be because it depends upon the design adopted. There is no corresponding knowledge of the covariance efficiency, which depends upon the randomisation. Usually it is not far short of 1.0, so quite a small reduction in the error mean square will make up for it, but it is a mistake to introduce covariates without a reasonable expectation that they will be effective.

Another question is the standard value of x to which all values of y are to be adjusted. Usually the general mean for x over the whole experiment is chosen, but there is no rule in the matter. If the intention is simply to find out what would have happened if the units had been uniform with respect to x, the conventional method is justified. Indeed GENANOVA suggests it, but the user is given the opportunity to adopt some other value if the problem requires it.

6.3 Double covariance

Sometimes the user will wish to introduce two covariates, w and x, instead of one. GENANOVA provides for that, but not for three or more. With more than one covariate there is a point to be noted, namely, the relationship between them. At first sight it is all right to say that a change of 1.0 in w will lead to a change of Ewy/Eww in y and a similar change in x will add Exy/Exx to the adjustment that has already been made, but the argument contains a flaw. Unless w and x are independent of one another, changing w will lead to a change in x, i.e. w can affect y not only directly but indirectly through x. That being so, the so-called total regression coefficients like Ewy/Eww and Exy/Exx must for the moment be set on one side. In their place are needed the partial regression coefficients, which show (1) what effect a change in w would have on y, x being held constant, and (2) the effect of x on y, w being held constant. By their use the double adjustment can be made. First w is changed with x constant at its initial value, then x is changed holding w constant at its new value. Such a double adjustment could well reduce the covariance efficiency below its value for a single adjustment. Also, since two regression coefficients are being estimated instead of one, the sums of squares for both the error and the stratum total lose a further degree of freedom.

In the extreme case w and x can be so closely related that one virtually determines the other. If that does happen, the method of double covariance breaks down. It makes no sense to talk of changing w, x being constant, in circumstances where a change in w necessarily implies that x changes too. Such a situation is called a collinearlity, because plotting the residuals of x against those of w will give a straight line exactly. Even if the collinearity is not completely perfect, the relationship between w and x can be so close as to give confusing results. What happens in GENANOVA is that the program works out the correlation coefficient between the covariates as a matter of course. If its square exceeds 0.9, w is discarded and the analysis reverts to a single covariance with x alone. A message is given to explain what has happened.

6.4 Pseudovariates

The analysis of covariance is often used with artificial sets of numbers (sometimes called pseudovariates, sometimes dummy variables and sometimes indicator variables) serving as covariates. A common instance arises with a missing datum in a variate y. One way of dealing with it is just to ignore or set as missing the unit from which it was lost, but another possibility is to form x as a pseudo-variate for the full design. In x all units have the value 0 except for the one with no datum and that is assigned the value 1. In y the gap is filled with any convenient number, such as zero. Now GENANOVA is used, with x as the covariate. It will be found that the resulting analysis of y adjusted by x is exactly the same as that given by ignoring the observation altogether. (It should here be recalled that analyses of variance do not estimate means but only contrasts between them.) Of course, it is easier in practice to use the analysis of variance, but if the reader likes to try out both methods on some convenient body of data, the exercise will provide a simple introduction to the use of pseudovariates. If two data are missing, double covariance is needed with a different pseudovariate for each gap.

A similar problem arises if two units become mixed and the experimenter does not know the individual data but can find their sum. (The situation arises if two samples contaminate one another or if two yields are accidentally amalgamated or if two labels are lost, so only the sum of the sample values is known.) In such a case the method is to form a pseudovariate, x, in which one of the units involved is assigned the value +1 and the other -1. For all other units x equals 0. With y the total of the two units is assigned to one of them and zero to the other. An analysis of covariance of y adjusted by x will apportion the total fairly between the two units. (There will of course be one degree of freedom fewer for the error. Also the covariance efficiency will in general be less than 1.0, so no one should argue that the situation has been restored.)

If three units are involved, two pseudovariates are needed. In w the three units are assigned the values, -2, +1, +1; in x they should be 0, +1, -1 in the same order. Then, in y the total is assigned to the first of the units involved and zero to the other two. The effect of w is to apportion the total between the first unit and the others, while x makes a right apportionment between the second and the third. (Again there is lost information.) Pseudovariates are given the standard value of 0, which is also the general mean.

Pseudovariates are often used instead of blocks to control local variation. If an incubator has four shelves, each able to take several units, one way of controlling variability is to use the shelves as blocks. Another is to use a pseudovariate, x being equal to 1 for the top shelf, 2 for the second and so on. Using the analysis of covariance there will be a loss of only one degree of freedom from the error instead of three. On the other hand, using the pseudovariate assumes a steady trend. Someone who wanted to allow for curvature might want to add w, equal to 1 (= 1²) for units on the top shelf, 4 (= 2²) for those on the second and so on. There is now a loss of two degrees of freedom from error and with only four shelves most people would prefer to use blocks and avoid assumptions about the form of the trend. However, if there were many shelves, the blocks could lead to the loss of more degrees of freedom than could be tolerated, whereas the pseudovariates would still lose only two.

The use of distances and squared distances is quite common, but the method suffers from the curvature being more marked at the ends than in the middle. For that reason some prefer the alternative relationship given by the following method. One end is assigned the angle of 0 degrees and the other 180. Intermediate locations are assigned proportionate angles. Thus, four equally spaced shelves would be assigned 0°, 60°, 120° and 180°. Two covariates would then be formed, w from the cosines of the angles and x from their sines. Hence, their values would be:

Shelf	Angle	W	x
Top	0	1.000	0.000
Second	60	0.500	0.866
Third	120	-0.500	0.866
Bottom	180	1.000	0.000

A double covariance adjustment on w and x will provide a valid analysis, though once again there is a loss of two degrees of freedom from the error, which is similar to losing three for blocks. The situation would however be different if there were more shelves. In any case there is no need for all units of a block to have the same values for the covariates. If units were formed by cutting successive pieces from a roll of material, the first could represent 0~degrees and the last 180, the others taking intermediate values. In that case each unit would have its own values for w and x and there would be no need of blocks. With pseudo-variates like these it is usual, though not essential, to adopt the general mean as the standard value.

The method can be used to control temporal differences as well as spatial. Anyone who was designing an experiment that was intended to continue for a long time might well call the first day 0° and the last 180°. Double covariance could then be used.

[TOP]

---

7. Bivariate Analysis

7.1 Introduction to bivariate analysis

7.2 An outline of the method

7.3 The bivariate diagram

7.4 Degrees of freedom

7.1 Introduction to bivariate analysis

So far there has been only one variate of interest. It is true that in the analysis of covariance other quantities have been introduced, called covariates, and they have been subjected to calculations resembling those of the analysis of variance, but they have not themselves been the subject of investigation. They are important only to the extent that they can explain and reduce error in the variate, which is of importance and interest. In bivariate analysis two variates are studied in association.

There can be good reason for doing so. To take an example, if measurements are taken on a set of similar plants, it is to be expected that their heights and spreads will be closely associated in a positive sense. (That is to say, the more the plant spreads, the taller it will be.) If there is a drought and the plants begin to wilt, a scientist might irrigate some but not others to observe the effect. As a result the irrigated plants will become more erect giving an increase in height, which may be non-significant, and a decrease in spread, also perhaps non-significant. Is it to be concluded that the water has had no effect? The feature of the data of greatest interest could be the way that the treatment has moved the two variates in opposite directions, one up and the other down, despite the underlying positive correlation. Taken together the two variates may tell more than they tell separately. It is to deal with such situations that the bivariate analysis of variance has been developed. It should be emphasised that it is needed chiefly in a context of testing rather than of estimation.

The central problem is this: Suppose that the regression coefficient, b, (See Section 6.2) is 1.5 and that a certain contrast has the value of +2.0 in the analysis of x. Then it can be expected to have a value of +3.0 in y. If in fact the value is +4.0, the discrepancy could be a chance effect but it is possible that the treatments are having a direct effect on y additional to what has come through x. Further, that direct effect can be estimated as +1.0. In the analysis of covariance the approach is to adjust y by x, but that is valid only if x is random and cannot have been affected by the treatments. In bivariate analysis it is assumed that the treatments may be affecting either or both of the variates and the aim is to study the total effect.

From the above it might be supposed that the order of the variates matters, but that is not so. If x and y are taken in reverse order, the same conclusions will be reached though by a different course.

7.2 An outline of the method

Given two variates, x and y, it is easy to plot one against the other. Usually the result is an elongated cloud inclined at an angle to the axes. For many purposes that is very informative. Perhaps no more examination is needed, but from the point of view of testing there is a difficulty. Two points may lie close together, but that of itself does not mean that they could be chance variants one of the other. If the line joining them cuts across the cloud, i.e. in the direction of least variability, they could be a highly significant distance apart. On the other hand, if the connecting line ran along the length of the cloud, i.e. in the direction of greatest variability, the separation of the points might well be dismissed as non-significant. There is the further point already mentioned, namely, that an effect that goes against the prevailing correlation is more significant than one that goes with it.

In bivariate analysis the variates x and y are transformed to others, X and Y, such that both X and Y have a variance of 1 and such that they are uncorrelated. Then if X and Y are plotted the resulting cloud will be a circle. Consequently, a shift in one direction will have the same significance as a shift of the same magnitude in any other direction. What is more, the usual rules of geometry will apply.

The required transformation of x and y to X and Y is easily carried out. First, X is formed from x, thus:

X= x/(Standard error of x)

Then y' is formed by taking y and eliminating from it the effect of x. Taking b (as in Section 6.2), it is enough to write y' = y - bx. Then

Y = y'/(Standard error of y')

and the transformations will have been found. Of course, X and Y are artificial and do not have the immediate intelligibility of x and y, the quantities actually measured. Nevertheless, they do have meaning. Thus, X is only x measured on a different scale, while Y represents the part of y that cannot be explained by x, again on a different scale. Unlike X it is measured from an arbitrary origin.

7.3 The bivariate diagram

The first step in a bivariate analysis of variance is the same as in the analysis of covariance. That is to say, analyses of variance and covariance are worked out for x², y² and xy. After that the changes begin. The sums of squares and products in the error line are used to evaluate b and the standard errors as a basis from which to derive the transformations for changing x and y to X and Y. They are then applied to the treatment means for x and y (adjusted if necessary for non-orthogonality and confounding) to give the corresponding means for X and Y, which are plotted against one another. The result is the so-called bivariate diagram. Those who like to visualise results will find it an invaluable aid in interpretation.

If there are two treatments, A and B, each will have a point on the diagram; the distance between them is called the displacement brought about by changing from one treatment to the other. For purposes of illustration it will be supposed that the transformations are

X = 0.5x and Y = 0.8y - 0.4x.

(The equations are quite arbitrary and are introduced only to show how the calculations proceed.) For A let the mean value of x and y be 5.0 and 4.0 respectively, then for that treatment X is 2.5 and Y is 1.2. For B let x = 7.0 and y = 3.0, then it follows that X = 3.5 and Y = -0.4. That is to say, the contrast of the first treatment minus the second equals -1.0 in X and +1.6 in Y. On the diagram the distance between the two points is

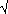{(-1.0)² + (+1.6)²} i.e. 1.89.

(It will be recalled that the ordinary rules of geometry apply.) The quantity 1.89 is called the displacement. Its significance can be tested by entering the contrast (+1, -1).

Incidentally, it may be noted that displacements are not altered by reversing the order of the two variates. Either way the treatment points will bear the same relationship one to another. The difference between the two bivariate diagrams lies in a change of origin and a rotation of the axes.

As has been said, the bivariate diagram lends itself to pictorial presentation. For example, if there are three treatments, A, B and C, representing equally spaced doses of some substance, the contrasts of interest are likely to be (-1, 0, +1) and (+1/2, -1, +1/2). The displacement due to the first is simply the distance between the points given by A and C. For the second, the comparison is between the result of B and the mean of A and C. The displacement therefore is the distance between the point for B and the midpoint of a line joining those for A and C.

Factorial designs likewise respond to pictorial representation. (At least, they do when all factors have two levels. Other cases can be more difficult.) Suppose for example that there are four treatments, (1), A, B and AB. Further, let treatment (1) give X- and Y-values that are respectively p and p'. If now the effect of A is to change those values to (p + a) and (p' + a'), while that of B is to change them to (p + b) and (p' + b'), in the absence of an interaction it is to be expected that AB will give an X-value of (p + a + b) and a Y-value of (p' + a' + b'). Hence, on the bivarate diagram in the absence of an interaction it is enough to take the points for (1), A and B and to find the expected point for AB by completing the parallelogram. The displacement is the distance between the point given by the data and the point just found, which was calculated on the basis of there being no interaction. It corresponds to the interaction contrast, i.e. (+1, -1, -1, +1).

7.4 Degrees of freedom

At this point a comment should be made about degrees of freedom. If an ordinary analysis of variance of x or y gives f degrees of freedom for treatments and e for error, in the bivariate analysis the corresponding numbers will be respectively 2f and 2(e - 1). Since each variate is subject to adjustment by the other, the loss of a degree of freedom from the error is to be expected, as in the analysis of covariance. Also, the doubling results from there being two variates, not one.

To consider the test of a displacement, it has two degrees of freedom. One corresponds to the value of the contrast in x, the other to its value in y after allowance has been made for x. (It could equally be said that one component corresponds to y and the other to x after allowance for y.) Whenever there are two degrees of freedom, it is always possible that a non-significant effect from one component will dilute a significant effect from the other, so it is by no means true that the bivariate test will be more sensitive than each of the univariate tests on x and y separately. If one variate is just a shadow of the other with no contribution of its own, it will not improve the bivariate analysis. On the other hand, including it may help to clarify the situation. For such reasons GENANOVA always gives all three analyses, the bivariate and both the univariate.

Last updated 23/04/03

© 2005 Statistical Services Centre ~ The University of Reading | Terms & Privacy | Feedback