Concepts Underlying the Design of Experiments
Release date: March 2000
This is one of a series of guides for research and support staff involved in natural resources projects. The subject-matter here is the design of experiments. Other guides give information on allied topics.
1. Introduction
5. Replication and levels of variation
7. Size and shape of plots in field experiments
8. Allocating treatment to units
10. Data management and analysis
1. Introduction
This guide describes the main concepts that are involved in designing an experiment. Its direct use is to assist scientists involved in the design of on-station field trials, but many of the concepts also apply to the design of other research exercises. These range from simulation exercises, and laboratory studies, to on-farm experiments, participatory studies and surveys.
What characterises the design of on-station experiments is that the researcher has control of the treatments to apply and the units (plots) to which they will be applied. The results therefore usually provide a detailed knowledge of the effects of the treatments within the experiment. The major limitation is that they provide this information within the artificial "environment" of small plots in a research station. A laboratory study should achieve more precision, but in a yet more artificial environment. Even more precise is a simulation model, partly because it is then very cheap to collect data. The limitation here is that the "model" is not "real": the results are limited by the parameters of the model and the extent to which it correctly represents reality.
It is easier to generalise from a well-planned on-farm trial in so far as the farms represent the recommendation domain, but there is less control over the treatments and plots. A survey makes generalisation easy, but with no control of the interventions to be explored. A participatory exercise gives detailed observations in a natural setting. A typical research project will involve a range of objectives that lead to a number of these types of studies.
The concepts of design are simplest to explain based on the design of on-station trials, partly because statistical methods were developed at a time when most experiments were of this type. So this guide should be of direct use for those who are planning an on-station exercise. It should also be of relevance to researcher-managed on-farm experiments where farmers' fields are "borrowed" to provide a more natural environment for investigating different treatment strategies relating to study objectives.
The control of treatments and plots is absent in a survey, where the researchers observe what "treatments", e.g. varieties and fertiliser levels, have been applied, but cannot dictate their application. Participatory on-farm research is often intermediary, because there can be some control. Here, in on-farm trials, the main effect of the default treatment is often not as interesting as the conditions under which some treatments fare better than others, or even as the characteristics of the plots used by farmers to decide on the application of particular treatments. This guide is therefore useful prior reading for those consulting the parallel guide on "On-Farm Trials - Some Biometric Guidelines".
We do not enter here into the debate on the relative merits of on-station or on-farm experimentation, or surveys, or participatory methods for conducting research. Our view is that they all have an important role, as do laboratory-based experimentation and computer-based modelling work. It is through a careful specification of the objectives that the best combination of research studies can be adopted, and many problems will demand a range of data-gathering exercises. One of our aims in writing short guides is to encourage researchers to be open to the use of the most appropriate type of study for their problems. We also believe that concepts that are standard in one type of research could often usefully be considered in another. For example, the concept of a "pilot study" is standard in the conduct of a survey and could be considered in many experimental programmes more formally than at present. In the other direction, the important concept of factorial treatment structure is a standard component of experimental work and can be used, both in the design and in the analysis of a survey or participatory study.
The main issues addressed in this guide are as follows:
(i) Identification of the objectives of the experiment in the form of specific questions.
(ii) The selection of treatments to provide answers to the questions. Statistical concepts of treatment structure are used to provide maximum information relating to these questions.
(iii) Choice of experimental units and amount of replication.
(iv) Control of the variability between sets of units through systems of blocking and/or by using ancillary information (i.e. covariate information) collected on the units.
(v) Allocation of treatments to particular units within the overall structure of units, involving, where possible, an element of randomisation.
(vi) Collecting data that are appropriate for the objectives of the research. These may be on the whole experimental unit, or may involve sampling within the unit.
2. Specifying the objectives
A review of the current situation is a preliminary to the setting up of research objectives, the aim usually being to identify knowledge gaps in the subject area being investigated and within these gaps to identify specific aspects that need to be explored. This should lead to a clear statement about the problem that needs investigating and hence to a specification of the objectives. It is also at this stage that researchers will decide whether an on-station trial is the research methodology to be adopted.
It is necessary to consider the resources that can be devoted to the experiment and useful to outline the form of the analysis so as to ensure that the experimental data can be analysed in a meaningful way. Paying attention to the way in which results are to be reported is also helpful in identifying whether the objectives have been clearly formulated. The preparation of a written statement of the objectives, listed in order of their priority, is the key to a resource-efficient and realistic experiment.
Different classes of objectives can be identified. At the simplest level, the experiment may be exploratory, for example finding what crops can grow in the favourable microclimate under a gao tree. Another type of objective is to develop a basic understanding of the factors that influence a major response, e.g. crop yields or milk production in dairy herds, so that levels of these factors that optimise the response can be identified.
Usually, the objectives involve a comparison of the effectiveness of different technologies and can be formulated in the form of testable hypotheses. These experiments involve taking particular action with some expectation about their results. For example, two new herbicides may be compared with a standard control herbicide with the expectation that the new herbicides would perform better in pest and weed control than the standard. Two hypotheses are of interest here: (a) new herbicides are superior to the control; (b) there is little difference in performance between the two new herbicides.
Ideally, the objectives lead directly to the treatments to be applied (Section 3), the measurements that will be needed (Section 9) and the analysis that will be undertaken. In practice we normally find that the process is iterative. For example once the treatments are discussed it is often found that the statement of the objectives requires modification.
3. Selection of treatments
3.1 Terminology
We shall first explain treatments, factors and levels, by considering three examples:
* An experiment to evaluate 24 varieties of cowpea.
* An experiment to evaluate 8 varieties under each of 3 different levels of fertility
* An experiment to evaluate 4 varieties at 3 levels of spacing, for 2 planting dates
These three experiments all have 24 treatments. In the first experiment there is just a single factor, the variety, which has 24 levels. Thus, in this simple case, whether we think of the different varieties as the treatments, or the levels of a treatment factor, makes no difference.
In the second experiment there are 2 factors, namely accession, with 8 levels and fertility, with 3 levels. Each treatment consists of taking an accession at a fertility level, thus there are 24 different combinations, or treatments. This is known as an "8 by 3" factorial treatment structure.
Similarly, the third experiment has 3 factors and the 24 treatments consist of a "4 by 3 by 2" factorial treatment structure.
It is also useful to distinguish between two "types" of factor. The 3 different levels of fertility in the second experiment might be 0, 50 and 100 kgs of P per ha. This is an example of a quantitative factor and might be used if the objectives concerned the most appropriate level of fertility to apply. In this case there is a clear ordering to the levels of the factor - 0 is less than 50 which is less than 100. Hence the presentation of the results would normally be in the same order. The actual levels used are normally arbitrary choices from a range and indeed one question on design might be whether these levels would be more effective than the use of 0, 40, 80 and 120 kgs/ha. The conclusions normally result from fitting a curve to the data and might be that 60kgs/ha is the estimated value to recommend, even though the experiment did not have a treatment that corresponded to this exact value.
With regard to quantitative factors, there are two main design questions: (i) how many levels, and (ii) which ones. Because a curve will normally be fitted to model the response from a quantitative treatment factor there is usually little point to having more than 3, or at most 4 levels of the factor, at the expense of another factor that may be included in the experiment. For example, instead of having the 6 levels, 0 25, 50, 75, 100, 150 of P, it would usually be better, for the same resources, to have fewer level of P, e.g. 3 levels at 0, 75 and 150, plus 2 levels of an additional factor.
Not all factors are quantitative. The variety factor, in the examples above, is a qualitative factor. In such cases there is often no particular ordering to the levels of the factor and the results are often presented in their yield order. In this case also the conclusions normally relate to recommending one or more specific varieties.
There are also intermediate cases, where the levels of a factor are ordered, for example a study of planting dates might have varieties that are chosen because of their maturity cycle, or degree of determinacy. In such cases the results would normally represent a particular group and would normally be presented in the order that is determined by this grouping, for example, maturity cycle.
We now look briefly at two important issues, namely the role and need for control (or baseline) treatments; and the role of factorial treatment structure.
3.2 Control treatments
Control treatments need to be justified, through the objectives of the experiment, in the same way as any other treatment. For example, having a "no fertiliser" control is useful if the objectives include assessing the gain from adding fertilisers. If, however the objectives relate purely to comparing organic and inorganic fertilisers then there may be no need for a treatment without either. As a second example, consider a mixed cropping experiment on maize and cowpea. If the objectives include evaluating the advantage of growing the crops together, compared to sole cropping, then the inclusion of sole crop plots is essential. If, on the other hand, the aims relate purely to the way in which the crops should be mixed, then strictly there is no need for sole crop plots within the trial. In this latter case it may still be useful to have some areas devoted to the sole crops, to report on the experiment as a whole. This is then similar "baseline" information to reporting on the soil and climatic characteristics of the experimental site. We return to this point in the section on measurements, because it relates to the type of unit on which measurements are made.
3.3 Factorial treatment structure
Some experiments, particularly breeding trials, have only a single factor. Often, however it is useful to consider more than one factor in an experiment and one of the examples earlier gave three factors, namely variety, spacing and planting date with a total of 24 treatments. In the discussion below, we assume this treatment structure with two replicates, that is an experiment with 48 plots.
The advantages of factorial treatment structure, compared with experiments that consider factors one at a time, are well established. These include the idea of hidden replication, plus the ability to study the interaction effects. In the example above, first suppose there are no interactions, then the main effects of each of the three factors is assessed by averaging the results over the levels of the other factors. For example, for the spacing factor that has three levels, these are each applied on 16 out of the 48 plots, hence there are 16 replicates of each level. This is the idea of hidden replication. There are just two explicit replicates but the replication is multiplied eight-fold, because the results for each level of the spacing factor can be averaged over the eight levels of variety by planting date.
Now suppose that there is an interaction between planting date and variety. Then the use of the factorial treatment structure has at least allowed us to detect its presence. We must look at the two-way table for the eight different combinations of date by variety. If this is the only interaction, then each of these eight effects has six replicates.
The case for factorial treatment structure is so strong that it should often lead to experiments with a reasonably large number of treatments. For example, if 48 plots are available then having two replicates of the experiment with 24 treatments, described above, will almost certainly be a better experiment than six replicates of the simpler experiment with just eight treatments from two factors.
Treatments chosen for experiments can also be "near-factorial" in their structure - i.e. a factorial set with perhaps an extra treatment or one or two combinations omitted. For example, a study of the application of different amounts of fertiliser (three non-zero levels) at different growth stages (three levels), might also include a "no fertiliser" control, making a total of 3*3+1 = 10 treatments. Alternatively, an NPK study might look at different combinations of N, P and K but omit the treatment which has the highest level of all three.
4. Choosing the sites
Whether the experiment is conducted at a research station or on farmers' fields, selecting the sites for the experiment needs careful attention. This is because the chosen site(s) determine the recommendation domain, to which the conclusions can be generalised. This is usually not a problem in fundamental research where the aim may be to determine the form of causative mechanisms that influence crop response to some external intervention.
In applied research, however, the conclusions from the actual sites should be similar to what would have happened within a wider recommendation domain of interest. Then the aim is to use sites that are representative of that domain, e.g. sites with the same soil type or season length. A different situation is where the objectives demand purposively selected areas. For instance, if new interventions to control disease or pest incidence are being investigated, it is necessary to choose sites that are known to have high levels of disease incidence or pest attack so that the effects of the interventions can be observed and evaluated.
The issue of how many sites to use is discussed in more detail in a parallel guide "Some basic ideas of sampling". A common procedure with on-station research is often to do an identical experiment at say three sites. This is simply a sample of size three in terms of generalising from these sites to a wider group of sites. Depending on the objectives, it may be better, for the same cost, to do a larger experiment at just one of the sites, and smaller trials at ten others.
On-station experiments are often repeated for two or three years, because of differences caused primarily by climatic variation. This is again a very small sample of years; one way to generalise is to use a simulation model of the problem being investigated. This can then use much longer historical or simulated series of climatic records. Even where such models cannot replace any component of the experiment they may still allow an assessment of the sensitivity of the experimental results to climatic variation or climatic change.
The characteristics within each site play an important role in determining the details of the experimental design. These details include the size, shape and orientation of the plots and the identification of blocks (See also sections 6 and 7 below). Typical sources of variability at potential sites are due to soils, topography and other physical features. It is important to take account of these sources of variation and minimise their effect when choosing areas for laying down the experiment and this may mean omitting parts of the site. Soil variability is generally the largest likely source of variation. Where resources permit, a uniformity trial or taking soil samples may help in identifying patterns in soil variability. A map of the site and information about its past history are useful.
5. Replication and levels of variation
A question frequently asked by experimental scientists at the design stage of the experiment concerns the number of replicates to be used. Experiments are usually aimed at comparing treatments. This almost always involves comparing their mean values - guidance on the number of replicates then follows from the formula for the precision with which a treatment mean is estimated.
The key
formula is that the standard error of a treatment mean is given by 
/
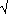n,
where is the
standard deviation of an individual observation and n is the number
of replicates. In the analysis of experimental data, ²
is estimated by the residual mean square in the Analysis of Variance table.
An effective experiment is one that permits precise comparisons to be
made; this is either one that has a small amount of unexplained variation
( is small) or
a lot of replication (n is large).
In practice we find that the number of explicit replicates used is often between 2 and 4 and adding a further replicate is then of comparatively little value. For example, changing replication from 3 to 4 makes comparatively little difference to (n in the formula above ((n changes from 1.7 to 2). There are two things that make a big difference. The first is the hidden replication from a factorial treatment structure; we saw an example in Section 3 where the replication of some comparisons was increased 16-fold in the absence of treatment interactions. The second is to concentrate on an effective design, namely one that has as small a value of ( as possible. You make ( small by trying to explain as much variation as possible. These explanations are done at the design stage, by using blocking (Section 6) and covariance (Section 9) effectively, and at the data collection and analysis stages by examining critically the measurements that have been made, particularly any extreme values.
In deciding
on the number of replicates, one requirement is that we should be able
to estimate the residual variation, 2
itself, with reasonable precision. To check this, it is useful to draw
up the basic structure of the analysis of variance table, listing the
treatment and block terms with their degrees of freedom. You should ensure
that the level of replication is sufficient to provide an adequate number
of degrees of freedom for estimating the experimental error variation.
A reasonable rule of thumb is to say that ten is a minimum, while much
more than about 20 d.f. is unnecessary. The latter may indicate an excessive
amount of explicit replication, and the inclusion of an additional factor
in the experiment might lead to a more efficient use of resources.
In considering replication, it is important to be clear about the experimental unit, and to ensure that there is sufficient replication of these units to allow the treatment comparisons to be made. Consider for example a tree species trial with five species, where there three plots per species, each with four trees. This gives a total of 60 trees in 15 plots. Growth rates are measured by recording initial and subsequent heights of individual trees. Here the experimental unit to compare species is the whole plot and not an individual tree. When comparing the species, it must be recognised that there are just three plots per species, even though we have 12 measurements of growth. Another example is a livestock study where treatments are administered via the drinking water to pens of animals, but weight gain is recorded for the individual animals in the pens. Here the experimental unit is the whole pen of animals, even though we have data at the individual animal level.
Thus the unit of replication is the unit to which the treatment is allocated. In the tree species example, differences between the species must be assessed relative to the plot-to-plot variation, not the tree-to-tree variation. The latter gives the within-plot variation while the former is the between-plot variation. Using the within-plot variation to compare species is not the appropriate level of variation. It may overestimate the between-plot variation (because of competition) or may underestimate it because of homogeneity of the within-plot environment.
Different levels of variation also occur in split-plot experiments. These are experiments where the size of unit needed for one treatment factor (say an irrigation treatment or a land preparation method) is larger than the size required for the other treatment factor (say crop variety). Here the irrigation treatment (say) is laid down in larger sized plots (called main plots) which are then split into a number of sub-plots to accommodate the different varieties under consideration. Two sources of variation exist here: the variation between main plots against which irrigation treatments must be evaluated, and the variation between split-units (within main units) against which variety differences and the interaction between irrigation levels and varieties must be assessed.
6. Choosing the blocks
The concept of blocking in experiments is the equivalent of stratifying in surveys. However, while stratification is used for a variety of reasons, e.g. to ensure that important sub-groups (wealth group, gender) are correctly represented, as well as just for administrative convenience, the main reason for using blocks in an experiment is to increase the precision of treatment comparisons. Thus it is rare for all the experimental material to be homogeneous, but often the experimental units can be grouped so that within a group (called a block) the units are homogeneous. Thus, in an animal experiment, animals within the same litter would be expected to give similar results; in a field experiment, plots physically closer to each other, or having similar soil properties, would be expected to give similar yields. The grouping of a set of experimental units into homogeneous sets (blocks) is referred to as blocking.
The experimenter's familiarity with the material to be used, and with past experiments of a particular type of experiment, should help in choosing blocks. For example, in an animal experiment the age, sex and breed are characteristics that might be relevant to the future performance of the animal. In experiments with field crops, fertility gradients in the field or physically defined variables such as moisture and water levels, height and slope of the land can all be candidates for blocking.
One common design is called the randomised complete block design. This is when the blocks are all the same size and this size is the same as the number of treatments in the experiment. In this case a block contains a single replicate of each treatment. This design remains useful but it is so common that scientists have sometimes confused the concepts of blocking and replication.
We would encourage researchers to look afresh at the way they block experiments, particularly now that there is easy-to-use statistics software to help in the design and analysis of such experiments. Blocks should consist of similar experimental units, and it is much more important to have homogeneity within blocks than for blocks to be of equal size and to be the same size as the number of treatments. In general, blocks of size two are the minimum and this is in common use, for example using the 2 sides of a leaf. In other situations, such as using the animals from the same litter as a blocking factor, the blocks are not of the same size.
Many on-station experiments involve more treatments than can be accommodated in homogeneous blocks, i.e. blocks often have fewer plots than there are treatments. This is familiar to breeders where it is generally not possible to include all of the large number of genotypes within homogeneous blocks. Incomplete blocks are the norm here and the tradition is of balanced lattice designs with block sizes equal to the square root of the number of genotypes being evaluated. Subsequent development of alpha designs has removed this restriction on the number of genotypes in relation to the block sizes.
The desirability of factorial treatment structure also leads to many treatments in an experiment. Small blocks are also possible with experiments that involve several factors by sacrificing information on one or more of the higher order interactions amongst the factors. Thus, less important information is confounded (mixed) with the block to block variation, while allowing all the important information to be estimated precisely, because of the homogeneity of the small blocks.
7. Size and shape of plots in field experiments
The choices of plot size and shape are governed primarily by practical issues. On plot size it is clear that, for a fixed available area, more replication can be achieved with smaller plots, e.g. one tree or one animal. However this must be balanced against the practical need for large plots. These may be for particular treatment factors, such as irrigation, or a mixture of crops. They may also be because of the types of measurement that are being taken, for example, on weeding times.
Similarly on plot shape, comparisons are more precise if, for a given area, plots are long and narrow because neighbouring plots are then very close together. However practical considerations (e.g. ease of cultivation or harvesting, type of equipment being used, etc) may dictate the need for square or rectangular plots. On particular types of land, other shapes may also be feasible, e.g. plots following the shape of the land contour in terraced land.
This all assumes, however that there is no need for border areas round each plot, because of the possibility of some carry-over of treatment effects from neighbouring plots. Where guard rows are needed, both small plots and narrow plots become inefficient, because they result in a greater proportion of the plot being wasted. In such cases square plots are common and they should be of such a size that most of the plot can be harvested and recorded.
8. Allocating treatment to units
The main issue here is the use of randomisation in allocating the treatments to the blocks. The principle of randomisation is important because it guards against possible, but unidentified sources of variation that may exist in the experimental material. It can be regarded as an insurance against results being biased due to unforeseen patterns of variation amongst the units.
However in some situations, practical considerations could well outweigh the statistical requirement for randomisation. For example, in siting control plots in an agroforestry experiment, trenches surrounding the plots may be needed to ensure non-interference from trees in neighbouring plots. If the control plots are placed in a corner of the experimental area, then trenches are needed only on two sides of the control plot, rather than on all 4 sides, thus limiting the effort needed in conducting the experiment.
There are also situations where the particular form of treatment does not allow randomisation. For example if the treatments were storage times or times for fermenting a particular substance, randomising the time element may not be possible. In these types of situation, the researcher has to feel reasonably comfortable in saying that the data can be analysed as though randomisation had taken place. In general, it is best to randomise the allocation of treatments to units or blocks wherever possible within the constraints of experimental resources.
9. Taking measurements
The general questions to be considered are which measurements best suit the research objectives; what additional measurement could be useful and at what scale; when will the measurements be taken; and how will the measurements be made and recorded.
Measurements are taken, i.e. data are recorded, for three broad purposes. The first is to give the overall context of the experiment. These are measurements such as the location of the trial, the dates of various operations and climatic and soil characteristics. These measurements are normally recorded for the experiment as a whole and enable users to see the context of the experiment and hence the "domain of recommendation", see Section 4. Often too little data of this type are collected.
The second and most important reason for taking measurements is to record the variables that are determined by the objectives of the trial. These are normally recorded at the plot level, i.e. the level at which the treatments were applied. They may be recorded at a still lower level, e.g. the tree or animal level, when the experimental unit consists of a group of trees or animals. Sometimes too much data are collected that do not correspond to any of the stated objectives.
The third reason is to explain as much variation in the data as possible. For example a yield trial with different species of millet suffers from bird or insect damage or water-logging in a few plots. Although these variables are not of direct interest in relation to the objectives of the trial, they are recorded, because they may help to understand the reasons for variability in the data. In the analysis they may be used as covariates or simply to justify omitting certain plots. Failure to make recordings of this type leaves differences due to these effects as part of the unexplained variation. This might make it more difficult to detect treatment differences, i.e. to realise the objectives of the trial.
When planning the measurements to be taken, it is important to clarify whether particular measurements will be taken at the experiment level, or at the plot (unit) level, or at the plant (sub-unit) level. For example soil measurements may be taken at the experiment level to characterise the site, or within each plot to include within the formal analysis.
Occasionally there are unplanned events that necessitate a review of the objectives of the trial. For example, if the rainfall is low, in a variety trial, should irrigation be applied? This would keep the stated objectives, but make it more difficult to specify the domain of recommendation for the experimental site. An alternative would be to reconsider the objectives and perhaps to study drought tolerance instead of yields. The new objective(s) would lead to different measurements from those planned earlier.
For any experiment, the measurements to be taken can thus be considered in three phases.
* Measurements taken before the experiment begins. These can be for two purposes. The first is to assess which site is appropriate for the trial and will often involve a small survey. The second purpose is to record the initial conditions before the trial begins, for example, soil constituents, animal weights or initial plant stand.
* Measurements taken during the course of the experiment. Possible measurements include labour use for different operations, weed weights, tree height, dry matter, quantity of food eaten by animals, animal weights, disease incidence, etc.
* Measurements taken at the end of the experiment, e.g. yields in crop trials, degree of damage in storage trials, wet/dry weight of fish in aquaculture experiments, germination rates in seed storage experiments or milk yields in comparison of diets in a livestock trial.
Sometimes it is not possible to measure the whole unit (plot) and a sample is taken from within each unit. For example:
* a soil sample may be taken for five plants within each plot,
* nitrogen content may be measured for 5 leaves for each of 3 bushes in each plot,
* grazing time may be recorded for 5 hours for each of 3 animals in each fenced area.
The general principles of sampling apply here, just as in a sample survey. Here there is effectively a small sampling exercise within each plot or unit and the aim is to use the sample to estimate the overall value for each whole plot.
Some measurements during the season are destructive. In general, it is best to avoid destructive sampling if possible as it leads to several practical difficulties, e.g. need for larger sized units, or altered competition within plots. Often a less precise non-destructive measurement may be useful as well as being economical in terms of costs and time for measurement, e.g. using a disease score on a scale of 0 to 9 rather than a precise measurement of the percentage of the plant that is diseased. When destructive samples are taken, consideration should be given to the simultaneous recording of a non-destructive measurement on the sample and the whole plot. This can then be used to adjust the value from the destructive sample where necessary.
Sometimes particular measurements, like soil moisture, are sufficiently expensive to take that it is not possible to record this information on all the plots and a subset must be taken. For an approach to deciding on an effective strategy here we refer readers to the guide on Some basic ideas of sampling, where the equivalent issue is of a sample survey, within which a subset of the respondents are observed in more detail.
10. Data management and analysis
This guide concentrates on the design, rather than the management and analysis of experimental data. Other guides deal with those topics. Here we mention just those aspects that can help in the design of future trials.
Good data management and archiving is useful, not just for the current trial, but also to help in the effective planning of future research. When planning a trial it is useful to look at features of past trials and also at past uses of the field that is proposed for the experiment. At the experiment level information is likely to be available (somewhere!) from soil samples conducted for past trials. Knowledge of the coefficient of variation (CV) from similar trials helps to assess the number of units that are required, while information on the effectiveness of blocking schemes can help in determining the need, or otherwise, for small block sizes.
Sometimes measurements taken routinely are shown to be of little value. This can suggest further research or the need to take alternative measurements. For example, soil chemical measurements are expensive to process and may be shown to have little value, while simple indicators of soil structure might be more useful.
11. Taking design seriously
A good example of taking design issues seriously is the following. The International Centre for Research in Agroforestry (ICRAF) in Kenya has run a 2-week workshop entitled "The Design of Agroforestry Experiments" since 1994. The topics covered included those in this guide plus those from the on-farm guide On-farm Trials: Some Biometric Guidelines. Initially participants and even some resource people wondered why a 2-week workshop should be devoted to design. Statistics courses traditionally concentrate more on analysis and the participants felt they needed help there. But by the end of each workshop all had realised the importance of devoting the time to the planning stage. The protocols they had brought for the forthcoming season had usually changed substantially. Agroforestry experiments are particularly complicated, but most of the same points apply equally to all fields of experimentation.
Last updated 14/04/03