Statistical Good Practice Guidelines

Statistical Guidelines for Natural Resources Projects

Date of publication : March 1998

This is the first in a series of guides for research and support staff involved in natural resources projects. The subject-matter here is general statistical guidelines. Other guides give information on allied topics. Your comments on any aspect of the guides would be welcomed.

  1. Introduction
  2. The Planning Phase
  3. The Data
  4. Analysis
  5. Presentation of Results
  6. Biometric Support

1. Introduction

This is the first in a series of guidelines for staff involved in the development and presentation of research projects. The guidelines are intended to help researchers to identify their biometric or statistical needs. This introductory guide gives general information, while other guides examine individual topics in more detail.

Our basic premise is that research projects can often be enhanced by improvements in the statistical components of the work. Areas where an understanding of statistical ideas is important include the following:

Without sufficient confidence in statistics, researchers plan designs that are often conservative, primarily to ensure a simple analysis. While this is sometimes appropriate, simple improvements can often result in more informative experiments or surveys for the same cost. Measurements may be made that are inappropriate for the objectives of the study, and are subsequently not analysed. Data entry can become a very time-consuming part of the study if it is not planned in advance. The analysis may be rushed, using inappropriate software, because of the pressure to produce results quickly. The study is then concluded, with the realisation that there is much more that can still be learned from the data. However, funding is at an end, and problems in the data management have made it difficult to allow easy access to the data, even for future researchers within the country where the study was made.

In this guide we consider these stages, from planning to presentation, in turn. Its aim is to encourage the researcher to think about the crucial aspects of planning, analysing and interpreting data. You may find methods referred to that are unfamiliar - this should certainly indicate that you might need advice. We conclude by describing further support that is possible by the involvement of a biometrician within the research team.

2. The Planning Phase

2.1 Specifying the Objectives

2.2 Units of Observation

2.3 Scope of the Study

2.4 Planning an Experiment

2.5 Planning a Survey

2.6 Other Types of Study

2.1 Specifying the Objectives

An initial step is to specify the areas where there are gaps in the existing knowledge and hence determine the types of research to be used. If there is insufficient knowledge of the constraints to adoption of a new technology, then a survey or an on-farm, participative experiment may be indicated. Lack of information, for example on critical processes affecting water use by proposed crops, might necessitate on-station, laboratory work or the use of a crop simulation model, or both. "Brain-storming" sessions among interested parties are often useful components of this initial process of identification of the areas and types of research that are needed.

In the protocol for the research study, gaps in current knowledge provide the basis for the background / justification section. A statement of the objectives usually follows this section. Sometimes there will be an overall objective, followed by a series of specific objectives. The objectives must be formulated with care, because they determine key features of the study design. For example, the treatments in an experiment follow directly from the objectives, as should the structure of the questionnaire in a survey.

2.2 Units of Observation

The units of observation are the individual items on which measurements are made. Examples include:

Some studies involve more than one type of unit. For example, a survey may collect data on households and individual farmers; an agroforestry experiment may apply treatments to whole plots and make some of the measurements on individual trees.

2.3 Scope of the Study

The scope of the study includes the population from which the units of observation should be selected. The concept of a "recommendation domain" - the population for which the conclusions of the study are to be relevant - is crucial.

Another important aspect is the size of the investigation. It is essential, before embarking on an investigation, to have an estimate of the precision of the answers that will be obtained from the investigation. At the simplest level the precision could be measured by the standard error of a difference between mean values, or between two proportions. However, it could also include precision of estimates of model parameters (rates of growth, dependence on time or on chemical concentration) or population parameters (proportion of arable land used effectively, percentage increase in uptake of new technologies by farmers).

Unless the investigation is expected to be capable of providing answers to an acceptable degree of precision it should not be started.

2.4 Planning an Experiment

Key characteristics of an experiment are the choice of experimental treatments to satisfy the study objectives and of the units to which the treatments are to be applied. There should be some control of sources of variation between the units - this is usually achieved by blocking. A randomisation scheme is used to allocate the treatments to the experimental units. For the treatments, the questions include

Control treatments provide baselines: the comparison of other treatments with a baseline is often an objective. However, controls are simply treatments, and their presence and specification must be justified just like any other treatment. On controlling variation, the questions include

In general a good experimental design ensures that the effect of treatments can be separated from the "nuisance" effects of environments with maximum efficiency. In designing an experiment, factorial treatment structure should be regarded as the norm. Also, designs using blocks with fewer units than there are treatments should be in common use.

In certain types of trial there are particular aspects of design which are important. For example:

2.5 Planning a Survey

The main elements of the design of a survey are a well-designed sample and a questionnaire (or other data collection procedure) which satisfies the study objectives. Crucial requirements of the sample design are representativeness and some element of randomness in the selection procedure. These usually imply a need for some structuring of the survey, often involving stratification, to ensure representation of the major divisions of the population. Deliberate (systematic) selection of samples can give, in general, the greatest potential accuracy of overall answers but has the disadvantage of giving no information on precision.

Some random element of selection is needed if we are to know how precise are the answers. In most practical situations clustering or multistage sampling will be the most cost-effective method of sampling. A balance of systematic and random elements in sampling strategy is usually necessary. In multistage sampling the largest or primary units often have to be selected purposively, but the ultimate sampling units are then selected at random within primary units.

For baseline studies the definition of sensible sampling areas, stratification scheme and the capacity for integrating data from varied sources are important.

In environmental sampling, where the spatial properties of variation are an important consideration, the spatial distribution of samples should provide information about variation at very small distances, at large distances and at one or two intermediate distances.

2.6 Other Types of Study

In observational studies, pilot studies and more empirical appraisal systems the general concepts of experiments and surveys are relevant although the particular detailed methods may not be applicable. Thus, representativeness and some element of random selection are desirable. It is also important to have some control, or at least recognition of potential sources of major variation.

Some studies also require access to routinely collected data, such as climatic records or aerial photographs. It is important to verify that these data are appropriate for the research task.

3. The Data

3.1 Types of Measurement

3.2 Collecting the Data

3.3 Data Entry and Management

3.1 Types of Measurement

Measurements can be made in many different forms ranging from continuous measurements of physical characteristics (weight, length, cropped areas) through counts (insects, surviving trees), scores of disease intensity or quality of crops, to yes/no assessments (dead, germinated) or attitudes (like, prefer). The importance of including a particular measurement has to be assessed in the context of the objectives of the research.

There are some general points which apply to all investigations.

3.2 Collecting the Data

Data collection forms will usually have to be prepared for recording the observations. In social surveys, the design and field testing of the questionnaire are critical components of the study plan. In experiments and observational studies, simple data collection forms often suffice.

3.3 Data Entry and Management

Part of the consideration of measurements is the question of how the data are to be managed. At some stage, the data will normally be held in one or more computer data files. It is important that the form of the data files and the software to be used for data entry, management and analysis are determined before data collection begins.

Data are sometimes collected directly into a portable computer. Where data collection sheets are used, the data entry should be done directly from these sheets. Copying into treatment order or "hand calculation" of plot values or values in kg/ha should not be permitted, prior to the data entry. All data should be entered: if measurements are important enough to be made, they are important enough to be computerised. Studies where "just the most important variables are entered first" inevitably result in a more difficult data entry process and the remaining variables are then rarely computerised.

Data entry should normally use a system that has facilities for validation. Double entry should be considered, because it is often less time consuming and less error-prone than other systems for data checking.

It is desirable to follow the basic principles of good database management. In some studies the management is a trivial stage, involving simple transformations of the data into the units for analysis. It can, however, present real challenges, particularly in multistage surveys or in animal, agroforestry or mixed cropping experiments. A general rule is to base the management on a series of programming commands, rather than using cut-and-paste methods. The latter often result in multiple copies of the data in different stages of the process, which make it very difficult to correct any errors that are later discovered when the data are analysed.

4. Analysis

In this section, more than previous ones, you may encounter unfamiliar statistical terms. These should emphasise that there are aspects of new statistical methodology from which you can benefit, with appropriate advice.

4.1 Initial analysis: Tabulation and Simple Graphs

4.2 Analysing Sources of Variation

4.3 Modelling Mean Response

4.4 Modelling Variance

4.1 Initial analysis: Tabulation and Simple Graphs

For experiments, initial analyses usually include simple tabulation of the data in treatment order, with summary statistics, such as mean values. For surveys, simple tables are produced, often showing the results to each question in turn. These initial results are only partly for analysis, they are also a continuation of the data checking process.

It is important to distinguish between "exploratory graphics", which are undertaken at this stage, and "presentation graphics", mentioned in the next section. Exploratory graphics, such as scatterplots or boxplots, are to help the analyst in understanding the data, while presentation graphics are to help to present the important results to others.

With some surveys, most of the analysis may consist of the preparation of appropriate multiway tables, giving counts or percentages, or both. Caution must be exercised when presenting percentages, making clear both the overall number of survey respondents and the number who responded to the specific question, as well as indicating which is used as the denominator.

4.2 Analysing Sources of Variation

Particularly for experimental data, an important component of the analysis of measurements is often an analysis of variance (ANOVA), the purpose of which is to sort out the relative importance of different causes of variation. For simple design structures, the ANOVA simply calculates the sums of squares for blocks, treatments, etc. and then provides tables of means and standard errors, the pattern of interpretation being signposted by the relative sizes of mean squares in the ANOVA. For more complex design structures (incomplete block designs, multiple level information) the concept of ANOVA remains the same, providing relative variation attributable to different sources and treatment means adjusted for differences between blocks. In studies with less formal structure it may be appropriate to split up the variation between the various causes by regression or, when there are multiple levels of variation, by using a powerful new method, known as REML.

The particular form of measurement will not tend to alter this basic structure of the analysis of variation, although where non-continuous forms of measurement are used the use of generalised linear models (a family of models which includes loglinear models and logistic regression) will usually be appropriate. Such methods are particularly appropriate for binary (yes/no) data and for many data in the form of counts. These methods are useful for all types of study - experiments, surveys and observational studies.

4.3 Modelling Mean Response

There are two major forms of modelling which may occur separately or together. The first form, which has been used for a long time, is the modelling of the mean response (for example, the response of plots of a crop to different amounts of fertiliser, or the response of an animal's blood characteristic through time). The objective of such modelling is to summarise the pattern of results for different input levels, or times, in a mathematical form which is consistent with the biological understanding of the underlying mechanisms. Frequently, the objectives also indicate the need to estimate particular comparisons or contrasts between treatments or groups. LSDs and other multiple comparison procedures should normally be avoided.

Modelling of mean response may also include multiple regression modelling of the dependence of the principal variable on other measured variables, though care should be taken to ensure that the experimental structure is properly reflected in the model. Note that, in modelling the mean response, the use of R² to summarise the success of the response model is usually not adequate. Large R² values need not reflect success in model fitting, which should be measured by the error mean square about the fitted model, relative to the expected random variation.

4.4 Modelling Variance

More recently modelling of the pattern of variation and correlation of sets of observations has led to improved estimation of the treatment comparisons or the modelling of mean response. Particular situations where modelling variation has been found to be beneficial are when variation occurs at different levels of units, for spatial interdependence of crop plots units or arrays of units in laboratories, or for temporal correlations of time sequences of observations on the same individual animals or plants.

Modelling of multilevel variation is beneficial when there is information about treatments from differences within blocks and between blocks, or when data from different trials with some common treatments are being analysed together allowing for variation between trials and within trials. The REML method, mentioned earlier, is relevant in all such cases. Multilevel modelling is also important for the correct analysis of survey data when the sample has a hierarchical structure.

Spatial analysis models have been found to increase information from field plot variety trials by between 20% and 80%. Essentially each plot is used to assess the information from adjacent plots.

When observations are made at several times for each animal in an observation trial, or for each plot in a crop growth study, it is crucial to recognise that variation between observations for the same animal is almost always much less than variation between animals. Analysis of such "repeated measurements" data must separate the between-animal variation from the within-animal variation in separate sections of the analysis. Several different approaches are available for the analysis of repeated measurement data, and they require thinking first about the general pattern of response through time, and analysing variation of that pattern.

5. Presentation of Results

The appropriate presentation of the results of the analysis of an experiment will usually be in the form of tables of mean values, or as a response equation. A graph of change of mean values with time or with different levels of quantitative input can be informative. Standard errors and degrees of freedom should generally accompany tables of means or response equations.

The results of survey analyses are usually presented as multiway tables of totals, counts or percentages.

For further advice, see the guide in this series called "Informative Presentation of Tables, Graphs and Statistics".

6. Biometric Support

Whenever a project involves the collection, analysis or interpretation of quantitative information it should be assumed that a biometrician or statistician may be able to help. This help is to make both the planning of the data collection, and the analysis, more efficient (in the sense of maximising the information per unit of resource).

The ideal situation is to include a biometrician as part of the research team. This is feasible if the research organisation includes a biometric support group. Ideally a named biometrician should be associated with each research project and should be involved from the earliest stage of planning in identifying the critical stages for biometric input. If no biometrician is available locally, then the leader of the research project should seek advice from a university, research institute or private consultancy, or from DFID's biometric advisers at the Statistical Services Centre.

The ideal is to use a biometrician or statistician familiar with the particular area of research, who will therefore have the experience of the particular scientific concepts and practical problems. If the biometrician does not have that detailed experience, both scientist and biometrician will have to explain concepts to each other.

Sometimes local biometricians are available, but they lack the necessary experience to make a substantial contribution unaided. There is no reason to expect more from a biometrician who has recently graduated with a Masters degree, than from an agronomist or soil scientist with a similar qualification. It remains important to try to use local expertise; the DFID biometric advisers can backstop such staff where necessary.

Glossary

This section contains definitions of possibly unfamiliar terms used in this guide. A list of recommended reference material is available online.

Biometrics
The application of statistical techniques in agriculture, ecology, forestry, fisheries, environmental science, health and medicine is often called biometry or biometrics. These terms derive from measurement (-metry) on living (bio-) organisms.
Experiment
A planned inquiry, conducted under controlled conditions. An experiment is generally aimed at comparing the effects of various alternative treatments, one of which is applied to each of a number of experimental units. One or more observations are subsequently made on each of the experimental units.
Survey
A research process in which new information is collected from a sample drawn from a population with the purpose of making inferences about the population in as objective a way as possible.
Population
The collection of all items under investigation (e.g. farms, individuals, field plots).
Size of the investigation
A common question for statisticians is how large a study needs to be. Scientists often seem disappointed that there is no universal answer. Cookbook methods of deciding "the sample size" are available for simple situations (e.g. for estimating a mean from a simple random sample taken from a population) but require knowledge of the variability and the degree of precision required in the estimation process. Applying such standard methods to more general situations is often misleading.
It should also be noted that the sample size question cannot be meaningfully posed unless there is one clear-cut objective in data collection which is agreed to be of over-riding importance, and a specific, predetermined form of analysis in which "the sample" will be used. This is usually not the case in reality. Working out a sensible disposition of the sampling effort, often compromising amongst several objectives, can be an effective part of the consultation with a statistician.
Standard error
The precision of an estimate (call it E say) is measured by its standard error. This is just the standard deviation of the values that E would take if a large number of repeat samples were to be taken and the estimate E calculated from data of each sample. The smaller the value of the standard error, the more precise is the estimate.
Factorial treatment structure
First some terminology, to explain "treatments", "factors" and "levels". Consider three examples:
  • An experiment to evaluate 24 genotypes of maize;
  • An experiment to evaluate 8 genotypes under each of 3 different fertility regimes;
  • An experiment to evaluate 4 genotypes at 3 levels of spacing, for 2 planting dates.
These experiments each have 24 treatments. In the first experiment there is just a single factor, the genotype, which has 24 levels. Thus, in this simple case, whether we think of the different genotypes as the treatments, or the levels of a treatment factor, makes no difference.
In the second case there are 2 factors, namely accession, with 8 levels and fertility, with 3 levels. Each treatment consists of taking an accession at a fertility level, thus there are 24 different combinations, or treatments. This is sometimes known as an 8 by 3 factorial treatment structure.
Similarly, the third experiment has 3 factors with the 24 treatments consisting of a 4 by 3 by 2 factorial treatment structure.
The two main reasons for using a factorial treatment structure are that they allow the researcher to study interactions between the factors and also that the "hidden replication" helps with the precision of the results from the experiment. These are both important concepts. Researchers who conduct factorial experiments for whom the idea of "hidden replication" is new, will probably find they can improve their experimental designs considerably.
Quantitative factor
A quantitative factor is a factor whose levels are quantitative measurements. For example, in an experiment to investigate the effect on maize yields from different plant spacings, spacing levels of (say) 60 cms, 80 cms, 100 cms will form three quantitative levels of the spacing treatment factor.
When an experiment involves one or more quantitative factors, the questions being asked by the experimenters are, or should be, also quantitative. Such questions are rarely answered appropriately by comparing pairs of treatment means. The use of three or more levels of a quantitative factor implies an interest in the response pattern of the observed variable to increasing amounts of the factor. The experimenter may be interested in estimating the level of the factor which produces the optimum response, or he/she may be interested in a more general description of the form of the response. In all cases, a proper first step is to plot the treatment mean responses against the quantitative levels and look at the pattern of response.
Blocking
Grouping experimental units into homogeneous sets (called blocks) improves the precision of treatment comparisons in a controlled experiment. Units within a block will be expected to behave similarly apart from naturally occurring variation. More details on this very important concept in experimental design can be found in the guide entitled "Design of Experiments".
Alpha designs
An extension of lattice designs without the restriction of requiring the number of treatments to be the square of an integer. Alpha designs (and traditionally lattice designs) are of value in constructing incomplete (small) blocks in situations where the number of treatments included in the experiment is large (e.g. variety trials with a large number of genotypes), and there is no well-defined treatment structure.
On-station and on-farm trials
For more details of on-station trials, see "The Design of Experiments". Ways in which experimental design concepts need to be adapted for on-farm research are explained in "On-Farm Trials", while "One Animal per Farm" deals with this special situation.
Sampling strategy
See "Some Basic Ideas of Sampling".
Good database management
See "Data Management Guidelines for Experimental Projects", Section 6.
Unfamiliar terms
The other guides in this series and the associated on-line information provide explanations of common statistical terms and detailed notes on a range of topics (although are not intended as a comprehensive glossary). The aim is to help researchers where no statistician is available and to give some supporting documentation to statisticians.
For those who would like more definitions, we recommend the glossary provided by the statistics teaching programme of the TLTP (Teaching and Learning Technology) Project. It is divided into 11 sections including "Basic definitions", "Presenting Data" and "Design of experiments", and can be found on the web at http://www.cas.lancs.ac.uk/glossary_v1.1/main.html
Simple tabulation of data
Tables are an effective way of presenting summaries of data such as counts (frequencies), percentages or other statistics, in tabular form. Simple tables present these summaries across one or two factor columns and lead to one-way and two-way tables.
The basic layout of a two-way table simply has columns and rows. A badly constructed table can be as confusing as a mass of data presented in narrative form. For presentation purposes, the same care should be taken with the construction of a table as with that of a graph. It is in many ways a work of art.
For further details, see Chapter 4 of W.M. Harper (1991) Statistics, 6th Edition, Longman Group (UK) Ltd., and E.R. Tufte (1986) The Visual Display of Quantitative Information.
Multiway tables
Multiway tables can arise in different ways. Such tables may merely be counts, percentages, etc. tabulated in two or more dimensions. Sometimes, the main table may be in two dimensions, e.g. farms classified according to the agro-ecological zone in which they are located and the gender of household head, with the villages nested within each zone. Here each village belongs to just one single zone, so villages and zones do not form a cross classification.
There are several ways of organising tables in three or more dimensions and decisions have to be made regarding the most effective presentation. There is no universal solution to this question. The appropriate table design will depend on the data and the objectives of the analysis.
Analysis of variance (ANOVA)
This is a frequently used statistical technique which models the variation in the response variable in terms of different sources of variation that are believed to influence the response. It is a technique that separates the total variation in the response into different components, each component representing some source of variation that influences the response. The underlying model that is fitted to the data is referred to as a General Linear Model. For further information see the guide on "The Statistical Background to ANOVA".
REML
The word REML stands for "Restricted Maximum Likelihood", the words Maximum Likelihood representing a statistical process that allows unknown parameters in a postulated model to be estimated. The REML procedure is an extension of the standard Maximum Likelihood procedure. It gives estimates of the variance components associated with a model involving multi-level data, i.e. data structures which occur at multiple stages of a hierarchy.
Generalised linear models
Standard analysis of variance techniques use an underlying General Linear Model where it is assumed that the residual variation, after allowing for all known sources of variation, are normally distributed. When the response variable has a non-normal distribution (e.g. Binomial, Poisson, Gamma), a Generalized Linear Model is used which models the data according to the type of distribution represented by the response being analysed.
Counts
Many experimental studies involve data collected in the form of counts, e.g. number of diseased plants in a plot, number of insects on a plant in a given period, etc. Counts are basically data that arise as integer values, ranging from 0, 1, 2 ... etc. or 1, 2, 3 ... etc. Such counts often follow a Poisson distribution and can be analysed using a Generalised Linear Model.
Particular comparisons
In experiments aimed at comparing a set of treatments having a structure of same kind (e.g. factorial treatment structure, a control treatment), it is advisable only to make pre-determined comparisons which address the specific objectives of the experiment. Details of constructing sensible comparisons and associated analysis procedures, can be found in the more detailed on-line document entitled Treatment Comparisons.
LSDs and other multiple comparison procedures
LSD stands for Least Significant Difference. It is a single statistic which allows all possible pairwise comparisons to be made and assessed for significance. Given a set of treatment means, if the difference between any two is greater than the LSD, then that difference is declared to be significant.
The LSD can be appropriate for an unstructured set of treatments. Although it appears routinely in refereed journals for experiments where the treatments are structured, it is not recommended in such situations, e.g. where treatments are quantitative (spacing levels, nutrient additions to animal feeds at increasing levels) or have a factorial structure (several varieties of a particular crop being tested with and without fertiliser).
Other multiple comparison procedures (e.g. Duncan's Multiple Range Test) are also used routinely but very often inappropriately. The dangers involved in the use of multiple comparison procedures is highlighted in Section 6 of the detailed on-line document entitled Treatment Comparisons.
Multiple regression modelling
Multiple regression modelling is often discussed in the context of one quantitative response variable being influenced by two or more quantitative explanatory (regressor) variables. However, both multiple regression models and analysis of variance models fall within the common theoretical background underlying the General Linear Model which assumes a normally distributed error structure. Such models attempt to explain variation in the response variable in terms of a mixture of qualitative or quantitative factors and a number of covariates (the quantitative regressor variables). Care must be taken to recognise the data structure in applying such modelling techniques so that account is taken of all known sources of variation.
Experimental structure is properly reflected in the model
Modelling the response variable using a general linear model or a generalised linear model is common in statistical analysis work. However it is important to incorporate all known sources of variation in the model. This in turn requires a careful assessment of the structure exhibited by the data being subjected to analysis. Different stratification variables must be recognised, e.g. data from different sites; farms according to gender of household head. Nested structures leading to multi-level data (e.g. animals within farms, farms within villages, and villages with districts) require allowing for the variability at different levels. Factorial treatment structures and blocking variables must be included in experimental work.
R²
R² is also called the multiple correlation or coefficient of determination. One way of thinking about R² is that it is the "square of the correlation between the data (Y) and its estimated values from the model". Another way of writing R² is
R² = (SS Regression)/(SS Total)
One problem with giving R² in its raw form is that if a variable is added to an equation, R² will get larger even if the added variable is of no real value. To compensate for this, the "adjusted" R² is often given as well. This is an approximately unbiased estimate of the population R², and is calculated by the formula
R² adjusted = 100(1- ssq(error)/(n-p)/ssq(total)/(n-1)).
This is roughly (1- the error mean square)/(total mean square) converted to a percentage. Here p is the number of coefficients in the regression equation. In the same notation, the usual R² is
R² = 100(1 - (SS Error / SS Total))
Error mean square
This is also called the Residual Mean Square. It is a component of an analysis of variance table and reflects an estimate of the natural (unexplained) variability in the response being analysed. The error mean square is used in estimating the standard error of treatment means and differences in treatment means (in experimental studies) and in estimating the standard error of predictions and other estimates derived from fitting a General Linear Model to the data.
Spatial interdependence
In field-plot experiments it is widely recognised that plots close to each other will tend to behave more similarly whereas those more widely separated will tend to be less similar in response to a given treatment. Measures of spatial interdependence attempt to summarise this pattern of similarity-dissimilarity.
Temporal correlations
There is some evidence that areas of a field which are relatively good in one year have a tendency to be relatively good in a following year; correspondingly poor areas tend to remain poor. A temporal correlation would be assessed by plotting, for a grid of areas within a field, the yields in year 1 against the yields in year 2. If the plot shows a positive trend then a degree of temporal correlation has been identified.
Variation at different levels
Many research studies involve taking measurements on different types of units. Consider a situation where units of one type (call them type A units) are nested within units of another type (call them type B). For example, in a typical on-farm experiment, data such as socio-economic characteristics of the farm, gender of household head, type of livestock on the farm, etc., are collected at the farm level. Nested within each farm, are plot level measurements such as the crop yields, disease incidence, etc. Here the full data set involved two sets of units, the farm units and plot units. Variation between farm units will clearly be different from variation between plot units. These two sources of variation form two levels of units which make up a hierarchical structure.
Variation at different levels is often referred to as Multilevel Variation. Recognising sources of variation at different levels is important as the different components of variation must be taken account of in the data analysis. In survey work, it is almost inevitable that variation will occur at multiple levels since many surveys are conducted as Multistage Surveys. They often include selecting primary units (e.g. districts), then selecting secondary units within each primary unit (e.g. villages), and further nested sets of units within each secondary unit such as farms within villages and field labourers within farms.
Spatial analysis models
A class of models for analysis of the variation between experimental plots which formally include terms representing spatial interdependence of plot results. A wide range of models has been developed during the last twenty years and many of these models are now available in major statistical packages. For large experiments the possibility of using a spatial analysis model for comparing treatments should be considered.
Repeated measurements
Such measurements arise when the same response variable is measured several times on the units to which various treatments have been allocated. For example in animal experiments, the degree of infection to some disease may be recorded, or blood samples taken, from each animal at weekly intervals, disease incidence on plants are often recorded on several occasions throughout the crop season. The specific characteristic underlying repeated measurements is that the repeat observations are not independent of each other since they are made on the same experimental unit. The analysis must therefore take account of the correlation structure amongst the repeated measurements.
Further details are provided in the on-line set of notes given in the document called Repeated Measurements.
Degrees of freedom
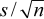The degrees of freedom reflect the number of independent pieces of information available to estimate variability. For example, the mean of n observations x1, x2, ..., xn made on a simple random sample drawn from an infinite population has standard error soverutn where s is the standard deviation of the set of observations. Here, the formula for calculating s is:
standerr
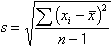
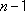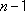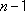Hence the standard error of the mean italxbar has nminus1 degrees of freedom. This is because the denominator used in calculating italic-s is (nminus1). The reason for subtracting 1 from the divisor of the above formula is that the italic-n differences in the numerator are not independent. They add to zero. Hence there are only (nminus1), rather than italic-n, independent pieces of information that can be used to compute the standard deviation. 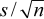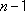Thus italic-s, and hence soverutn (the standard error of italxbar) are said to have nminus1 degrees of freedom.
DFID
The British Government's Department for International Development, formerly called ODA (Overseas Development Administration), which is responsible for promoting development and the reduction of poverty. DFID is funding the production of these guides, which are intended primarily for research and support staff involved in DFID projects.
Statistical Services Centre
The Statistical Services Centre is a non-profit-making centre attached to the Department of Applied Statistics, at The University of Reading, UK. The Centre employs its own staff and undertakes training and consultancy work for clients outside the University. Its staff advise DFID on biometric inputs to natural resources projects with the aim of supporting their effective design and implementation.

Last updated 23/04/03