Confidence and Significance: Key Concepts of Inferential Statistics
Release date: March 2001
This is one of a series of guides for research and support staff involved in natural resources projects. The subject-matter here is the confidence and significance - two key concepts of inferential statistics. Other guides give information on allied topics. Your comments on any aspect of the guides would be welcomed.
- Introduction
- Applying Estimation Ideas
- Standard Errors
- Confidence Intervals
- Hypothesis Testing
- Sample Size
- Non-Parametric Methods
- Analysis of Variance
- A General Framework
1. Introduction
In this guide we review the basic concepts of estimation and hypothesis, or significance, testing. Our aim is to discuss the key ideas of statistical inference in a way that is easy to understand. These are topics we would usually like to assume, when discussing or giving courses on data analysis for researchers. However, we often find the ideas are poorly understood and this lack of understanding contributes to the scepticism felt by some scientists of the role of statistics in their work. You could use the following three questions to decide whether you need to read further.
| True | False | Not sure | ||
| 1. | The standard deviation and the standard error are both used to summarise the spread of the data |  |
 |
 |
| 2. | The 95% confidence interval for the mean is the interval that covers roughly 95% of the observations. |  |
 |
 |
| 3. | If the difference between the effects of two farm management practices is not statistically significant, the conclusion is that there is no difference between them. |  |
 |
 |
If you have confidently replied false to the three questions above you may have little need to read this guide. Question 1 is discussed in Section 3, Question 2 in Section 4 and Question 3 in Sections 5 and 6.
For simplicity, we use "artificially small problems" to illustrate the ideas. In Sections 2 to 6 we cover the basic ideas of estimation, namely standard errors, confidence intervals, and hypothesis testing procedures. In the later sections we apply the ideas. We outline the way in which the sample size can be chosen. We also give our views on the role of non-parametric methods and on the implication of performing many tests on the interpretation of p-values. One reason that these two contentious issues are included is that they sometimes sidetrack training courses and discussions of other topics, because of researchers' strongly held views.
The general concept of statistical modelling is introduced in the final section of this guide. This provides a link to our other guides on analysis, and particularly to the one called Modern Methods of Analysis.
2. Applying Estimation Ideas
Estimating characteristics of a population of interest, from a sample is a fundamental purpose of statistical work, whether the activity is a survey, an experiment or an observational study.
Point estimation arises when a quantity, calculated from the sample, is
used to estimate a population value. The sample estimates
of the population mean (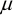 )
and standard deviation (
)
and standard deviation (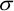 )
are most often taken as the sample mean,
)
are most often taken as the sample mean, 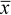 ,
and the sample standard deviation,
,
and the sample standard deviation, 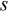 ,
where
,
where
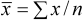 and
and
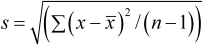 respectively.
respectively.
For example, consider estimating the average maize production per farmer among (the population of) smallholder farmers in a selected agro-ecological region. To do this, suppose a sample of 25 farmers is randomly selected and their maize yields are recorded. The average of the resulting 25 yields are calculated, giving say 278 kg/ha. This value is then taken as the estimate of the average maize production per farmer in the selected region. It estimates what one would expect for an individual farm. Similarly the sample standard deviation is an estimate of the amount of variability in the yields from farm to farm.
Other
estimates of the population mean are possible. For example, in many
surveys the observations are not sampled with equal probability.
In this case we might use a weighted mean 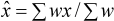 instead of
instead of 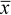 ,
with weights,
,
with weights, 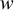 ,
that compensate for the unequal probabilities.
,
that compensate for the unequal probabilities.
Proportions can also be estimated, for example we may wish to estimate the proportion of families who own their own land, or the proportion of respondents who indicate support for community co-management of neighbouring forest areas during a semi-structured interview. Then we might use p = m/n, as the estimate, where m is the number of persons making a positive response out of the n who were interviewed. For example, if m = 30, out of n = 150 interviews, then we estimate the proportion as p = 0.2, or 20%.
As
a point estimate this is the same as a measurement, x, where
x = 1 if community co-management was supported and zero otherwise.
The estimate, p is then the same 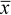 ,
given earlier, despite the "data" originally being "non-numeric".
Much qualitative material can be coded in this way.
,
given earlier, despite the "data" originally being "non-numeric".
Much qualitative material can be coded in this way.
If we have a contingent question, a follow-up only for those who "qualify" by supporting co-management, we might find, for instance, k = 12 out of the m = 30 who are prepared to play an active role in co-managing forest reserves. Arithmetically, r = k/m = 12/30 = 0.4 has the form of a proportion, but it is actually the ratio of two quantities which might both change if another sample of size n is taken in the same way from the same population. If the follow-up question is important, then we must ensure that the original sample is large enough that there are an adequate number of respondents who qualify (here there were 30) for the precision required of the study.
Sometimes
our main objective is not to estimate the mean. For example, in
recommending a new variety of maize to farmers we may wish to ensure
that it gives a better yield, compared to the existing variety for
at least 90% of the farmers. One way to proceed is first to calculate
the difference in yields for each farmer. If, from experience, or
from our sample, we can accept a normal model, i.e. that
the population of yield differences has approximately a normal distribution,
then the required percentage point is found (from standard statistical
tables) to be 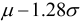 ,
where
,
where 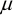 is the
mean difference and
is the
mean difference and 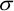 is
the standard deviation of the differences.
is
the standard deviation of the differences.
In
this case we can still use our estimates of 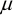 and
and 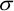 to estimate the required percentage point, or any other property.
In general we call the (unknown) quantities
to estimate the required percentage point, or any other property.
In general we call the (unknown) quantities 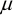 and
and 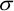 the parameters of the model. If we assumed a different probability
model for the distribution of the yields, then we would have to
estimate different parameters. The formulae would change, but the
ideas remain the same.
the parameters of the model. If we assumed a different probability
model for the distribution of the yields, then we would have to
estimate different parameters. The formulae would change, but the
ideas remain the same.
If, in the example above, we were not prepared to assume any distribution, then we could still proceed by merely ordering the differences in yields for each farmer and finding the value exceeded by 90% of the farmers. This is a non-parametric solution to this problem and we return to this approach in Section 7. Generally this approach requires more observations than a "parametric" or "model-based" approach, such as that in the preceding paragraphs.
For
reference later we explain the term degrees
of freedom. This is roughly "pieces of information".
For example, with the sample of 25 farmers we discussed earlier
we have a total of 25 pieces of information. In any study it is
usually important to have sufficient pieces of information remaining
to estimate the (residual) spread of the population. In our simple
example the spread is estimated by 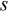 ,
and in the formula we divided by (n-1). This is because the
spread is being measured about the sample mean,
,
and in the formula we divided by (n-1). This is because the
spread is being measured about the sample mean, 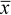 .
The sample mean is one of our 25 pieces of information, so we have
n-1 or 24 degrees of freedom left to estimate variability.
.
The sample mean is one of our 25 pieces of information, so we have
n-1 or 24 degrees of freedom left to estimate variability.
[TOP]
3. Standard Errors
When something is estimated, it is important to give a measure of precision of the estimate.
The measure of precision of an estimate is called the standard error of the estimate. The smaller the standard error, the greater is the precision of our sample estimate. Thus a small standard error indicates that the sample estimate is reasonably close to the population quantity it is estimating.
As
an example, suppose we select a random sample of 12 farmers (n
= 12) and measure their maize yields per hectare, we might find
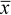 = 1.5
tons/ha and
= 1.5
tons/ha and 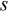 =
0.6 tons. Then our estimate of
=
0.6 tons. Then our estimate of 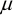 is given by
is given by 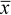 = 1.5 tons and its standard error (s.e.) is given by the formula
= 1.5 tons and its standard error (s.e.) is given by the formula
s.e. =
.
In
this case it is 0.6 / ![]() 12
= 0.17 tons/ha.
12
= 0.17 tons/ha.
From
the above formula it is clear that we get precise estimates either
because the data have small variability (i.e. 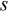 is
small) or because we take a large sample, (i.e. n is large).
For example, if, instead we had taken a larger sample of 108 farmers
that had given rise to the same mean and standard deviation, then
the standard error of the mean would have been 0.058. Equally, if
yields had been less variable at
is
small) or because we take a large sample, (i.e. n is large).
For example, if, instead we had taken a larger sample of 108 farmers
that had given rise to the same mean and standard deviation, then
the standard error of the mean would have been 0.058. Equally, if
yields had been less variable at 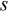 =
0.2 tons/ha then with 12 farmers, we would also have had an s.e.
of 0.058.
=
0.2 tons/ha then with 12 farmers, we would also have had an s.e.
of 0.058.
Depending on the investigation, we are often interested not so much in means, but in differences between means (e.g. differences in mean yield). In simple situations - where there is equal replication of the treatments and n replicates per treatment - the standard error of the difference between two means is
i.e. about one-and-a half times the standard error of each individual mean.
The formulae for the standard error of a proportion or a ratio that were considered in Section 2 are more complicated, but the point about precision being related to sample size and variability of the data is general. When the design of the study is complex, standard errors cannot be easily computed by "hand" and suitable software is used to obtain standard errors for estimates of interest such as treatment differences.
In this section we have repeatedly mentioned that the data are a random sample from the population. The reason that randomness is important is that it is part of the logic of the standard error formulae. This logic is that, because our sample was collected at random, it is one of many that might have been obtained. Typically each sample would have given a different mean, or in general a different estimate. The standard error measures the spread of values we would expect for the estimate for the different random samples.
The
idea of the standard error as a measure of precision can help researchers
plan a data collection exercise. In any study, 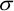 is the unexplained, or residual, variation in the data; and
an effective study is one that attempts to explain as much of the
variation as possible. Continuing the example above, we might find
that the farmers use four different production systems, thus giving
us two components of variation. There is variation between one production
system and another, and there is variation between the farmers within
a production system.
is the unexplained, or residual, variation in the data; and
an effective study is one that attempts to explain as much of the
variation as possible. Continuing the example above, we might find
that the farmers use four different production systems, thus giving
us two components of variation. There is variation between one production
system and another, and there is variation between the farmers within
a production system.
Suppose
the overall variation of the yields, ignoring the different production
systems, is estimated as 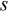 =
0.6 tons/h while the within production-system variability is
=
0.6 tons/h while the within production-system variability is 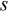 =
0.2 tons/ha. If we were planning a new investigation to estimate
average maize production we could either ignore the fact that there
are different production systems and take a simple random sample
from the whole population, or we could take it into account and
conduct a stratified study. The standard error formula shows us
that in this instance we would need nine times more farmers in the
simple random sample compared to the stratified study to get roughly
the same precision.
=
0.2 tons/ha. If we were planning a new investigation to estimate
average maize production we could either ignore the fact that there
are different production systems and take a simple random sample
from the whole population, or we could take it into account and
conduct a stratified study. The standard error formula shows us
that in this instance we would need nine times more farmers in the
simple random sample compared to the stratified study to get roughly
the same precision.
The guide on Informative Presentation of Tables, Graphs and Statistics describes how the standard error is used in the reporting of the results. The next section of this guide, which is on confidence intervals, shows how the standard error is used to describe precision. The width of a confidence interval is often a simple multiple of the standard error.
[TOP]
4. Confidence Intervals
The confidence interval provides a range that is highly likely (often 95% or 99%) to contain the true population quantity, or parameter that is being estimated. The narrower the interval the more informative is the result. It is usually calculated using the estimate (see Section 2) and its standard error (see Section 3).
When
sampling from a normal population, a confidence interval for the
mean 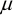 can be
written as
can be
written as
where
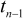 is the appropriate percentage point of the t-distribution
with (n-1) degrees of freedom. (See Section 2 for a brief
explanation of degrees of freedom)
is the appropriate percentage point of the t-distribution
with (n-1) degrees of freedom. (See Section 2 for a brief
explanation of degrees of freedom)
The 95% confidence interval is commonly used, for which t-values are 2.2, 2,1 and 2.0 for 10, 20 and 30 degrees of freedom. So we can usually write that the 95% confidence interval for the mean is roughly:
The
example in Section 3 involving 12 farmers gave 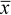 = 1.5 tons with s.e. = 0.17. The 95% confidence interval for
= 1.5 tons with s.e. = 0.17. The 95% confidence interval for 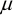 is therefore about 1.16 to 1.84 tons/ha; and so we can say that
that this range is likely to contain the population mean maize yield.
(The exact 95% interval, which one can get from a statistical software
package, is 1.12 to 1.88 tons/ha.)
is therefore about 1.16 to 1.84 tons/ha; and so we can say that
that this range is likely to contain the population mean maize yield.
(The exact 95% interval, which one can get from a statistical software
package, is 1.12 to 1.88 tons/ha.)
More generally, for almost any estimate, whether it be a mean, or some other characteristic, and from almost any population distribution, we can write that the 95% confidence interval is roughly
estimate
2
s.e.(estimate)
Hence it is useful that statistical software routinely provides the standard error of estimates. With the example of Section 2 of p = 30/150 = 0.2, or 20% of the 150 farmers the standard error is about 0.03, resulting in a confidence interval of about 0.14 to 0.26.
Note
what a confidence interval is and is not. A 95% confidence interval
does not contain 95% of the data in the sample that generated
it; very approximately the interval 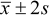 would do that. This is sometimes called a prediction, or tolerance
interval. In our examples of 12 or of 108 farmers above, with
would do that. This is sometimes called a prediction, or tolerance
interval. In our examples of 12 or of 108 farmers above, with 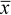 = 1.5 tons and
= 1.5 tons and 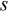 =
0.6 tons, this interval is 0.3 to 2.7 tons/ha and we would say that
most of the farmers have yields in this range.
=
0.6 tons, this interval is 0.3 to 2.7 tons/ha and we would say that
most of the farmers have yields in this range.
Users often confuse the confidence interval for the mean with an interval containing most of the data because the objectives of the study often relate to parameters other than the mean. This was considered briefly in Section 2.
In our example above, the 95% confidence interval for the mean is 1.12 to 1.88 tons with the sample of 12 farmers. With more data, this interval would be narrower as is seen by comparison with the confidence interval for a sample with 108 farmers, where the same calculations as above give a 95% interval for the mean of about 1.4 to 1.6 tons.
When the assumptions about the data may not be quite right, scientists may feel they ought to abandon the ordinary confidence interval and use some different procedure altogether. Usually it is more constructive to proceed instead by using the usual method, but noting that the true coverage of the "95%" confidence interval may not be exactly 95%. For most purposes, the 95% figure is used to provide a conventional measure of uncertainty about an estimate, rather than the basis for decision-making. The communication of the approximate magnitude of the uncertainty is usually more important than the exact value.
[TOP]
5. Hypothesis Testing
5.1 A Simple Example
5.2 Understanding Significance
5.3 General Ideas
5.1 A Simple Example
For good reasons, many users find hypothesis testing challenging; there is a range of quite complex ideas. We begin with a simple example.
A researcher facilitates an on-farm trial to study the effect of using Tephrosia as a green manure for fertility restoration. She claims the use of the manure will increase pigeon pea yields, i.e. pod weight. In the trial pigeon peas are grown with and without the Tephrosia in two plots on each of eight smallholders' fields and the values recorded are the differences in yields.
We
test the correctness of this claim. In this case the "null
hypothesis" is usually that the true mean increase, 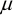 = 0. By the "true" mean increase we mean the increase
for the population of farmers of which we assume our eight are a
random sample.
= 0. By the "true" mean increase we mean the increase
for the population of farmers of which we assume our eight are a
random sample.
The alternative hypothesis is usually that the true mean increase is other than zero.
The null hypothesis is often given, as here, quite explicitly, with the alternative hypothesis being vague. This is for two reasons:
(i) Standard statistical tests calculate the probability of getting a sample as extreme as the one observed, assuming the null hypothesis is true - this calculation has to be done using explicit values for the parameter(s) of the null hypothesis distribution;
(ii)
Hypothesis testing adopts the same legal presumption of "innocence
until proven guilty". This is that the null hypothesis that
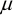 = 0 is to
be kept, unless the data values are inconsistent with it.
= 0 is to
be kept, unless the data values are inconsistent with it.
Textbooks
often distinguish between one-sided and two-sided tests. In this
example we might consider the test of the null hypothesis, that
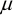 = 0, against
the one-sided alternative that
= 0, against
the one-sided alternative that 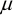 > 0, on the assumption that there is no logical reason that the
manure will decrease yields. Usually a one-sided test merely halves
the significance level, so what was significant at 4% with a two-sided
test, becomes significant at 2% with a one-sided alternative. As
will be seen below, we are not keen for readers to become too attached
to a particular significance level, so halving a value is not important
enough for users to spend much time on this idea. One-sided tests
are also rarely found in realistic situations, such as those introduced
later in this guide.
> 0, on the assumption that there is no logical reason that the
manure will decrease yields. Usually a one-sided test merely halves
the significance level, so what was significant at 4% with a two-sided
test, becomes significant at 2% with a one-sided alternative. As
will be seen below, we are not keen for readers to become too attached
to a particular significance level, so halving a value is not important
enough for users to spend much time on this idea. One-sided tests
are also rarely found in realistic situations, such as those introduced
later in this guide.
Example 1
Suppose in the illustration above, the differences in pod weight (in kg) between "treated" and "untreated" plots were as follows:
|
3.0 |
3.6 |
5.4 |
-0.4 |
-0.8 |
4.2 |
4.8 |
3.2 |
A computer analysis of these data would look like:
Test
of mu = 0 vs mu not = 0
Variable |
N |
Mean |
StDev |
SE Mean |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
The t-test used to investigate the hypotheses follows the general formula:
(estimate - hypothesised value) / s.e.(estimate)
Here we are interested in the mean difference in pod weight, so our test statistics is:
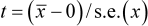
i.e. (2.87 - 0)/0.81 = 3.55
By
comparison with the 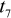 distribution, a value as extreme as 3.55 has a probability 0.009,
i.e. less than 1 in 100, of occurring. So, if the null hypothesis
is true, then there is a chance of just less than 1 in 100 of getting
the sample we found. Either something unlikely has occurred or the
null hypothesis is false. This event is sufficiently unlikely that
we declare the result to be statistically significant and reject
the null hypothesis.
distribution, a value as extreme as 3.55 has a probability 0.009,
i.e. less than 1 in 100, of occurring. So, if the null hypothesis
is true, then there is a chance of just less than 1 in 100 of getting
the sample we found. Either something unlikely has occurred or the
null hypothesis is false. This event is sufficiently unlikely that
we declare the result to be statistically significant and reject
the null hypothesis.
In Section 4 on confidence intervals we used a "t-value" of 2 to give approximate 95% confidence intervals. Similarly we find here that values larger than 2 are extreme, (at about the 5% level of significance) and hence cast doubt on the hypothesised value.
5.2 Understanding Significance
The classical argument is that we should approach this type of decision-based testing in an objective way, by pre-setting the significance level, or p-value at which we would choose to reject the null hypothesis. If we were working to a significance level of 5%, or p = 0.05, we would reject it at the 5% level and report that p < 0.05. Rather than following such a stringent approach, we recommend that decisions be made on the grounds that a p-value is low.
Example 2
We have the same hypothesis as in Example 1, but suppose we collected a slightly more variable sample. The data values might be:
|
3.0 |
3.6 |
6.8 |
-1.6 |
-2.0 |
5.8 |
7.1 |
0.3 |
Computer analysis of these data gives the following results:
Test
of mu = 0 vs mu not = 0
Variable |
N |
Mean |
StDev |
SE Mean |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
The standard error of the mean is now larger than in Example 1, and we get a t-statistic of 2.23 with a probability of 0.061. If we used the 5% level as a strict cut-off point, then we would not reject the null hypothesis. This does not mean we accept the null hypothesis as "true" and users who write as if it does are showing a serious weakness of interpretative skills. The probability of getting such a sample under a hypothesis of no effect is still low so there is some suggestion of a treatment effect, but not low enough to meet our criterion at the 5% level.
Here there is insufficient weight of evidence to draw a conclusion about a difference between the treatments. Had a sample of 16 observations been collected, with the same mean and standard deviation as above, the standard error of the mean would have been lower (at 0.91) and consequently the t-statistic higher (at 3.15). This would have been significant with a p-value of 0.007.
Note that if hypothesis-testing is undertaken because a real decision is being made - to accept or reject a new variety, for example - not rejecting the null hypothesis may be tantamount to accepting the pre-existing variety. This is not the same thing as accepting that the null hypothesis is correct.
Generally, scientific research does not involve such cut-and-dried decision alternatives. The main purpose of significance testing may just be to establish that an expected effect ("research hypothesis") can be discerned and plausibly shown; not just to be a quirk of sampling. Very tiny effects can be significant if sample sizes are very large; a significant effect also needs to be large enough to be of practical importance before it is "significant" in the ordinary-language use of the term.
Conversely, a non-significant effect does not necessarily imply that an effect is absent. A non-significant result can also happen if the sample size is too small or if there is excessive variability in the data. In either of these cases, the effect may in fact be present but the data is unable to provide evidence-based conclusions of its existence.
Such considerations show it is usually more informative to produce a confidence interval rather than just the decision outcome and p-value of a hypothesis test. In example 1 above, the 95% confidence interval for the mean is given by 0.96 to 4.79 using the method of calculation shown in Section 4. This indicates that the true mean increase of 0 kg is unlikely, because the 95% confidence for the true mean does not contain the hypothesised value.
Given a calculated t-value or other test statistic, it was traditional to compare this with a 5%, 1%, or 0.1% value in statistical tables. However, since many statistical packages compute exact p-values, results may be accompanied by statements such as (p = 0.028) giving a specific numerical figure for the degree of extremeness of the disparity between observed results and null hypothesis expectation. This approach is preferable where possible. It is more informative and easier to interpret.
5.3 General Ideas
In a few studies, the objectives of the study correspond to standard hypothesis (or significance) tests. The examples in the previous section provide one scenario and the adoption of a new farming practice, instead of a standard, is another.
Usually however, the hypothesis testing is just a preliminary part of the analysis. Only rarely can the objectives of a study be met by standard significance tests. The statistically significant result provides objective evidence of something interesting in the data. It serves as a "passport" to further analysis procedures. Confidence intervals or an economic analysis are then used to describe the nature and practical importance of the results.
When results are "not-significant" it may indicate that nothing further need be done. Often it enables a simpler model to be used. For example if there is no evidence of a relationship between education level and adoption of a new innovative technology, then the adoption can be studied using all respondents together. If there were a relation then it might indicate the necessity for a separate analysis (i.e. a separate model) for each education level group.
5.4 Recognising Structure
Example 1 above illustrates how a t-test is conducted using differences between plots from eight smallholder farms. The differences were used because a pair of plots was available from each farm. This led to a paired t-test.
Suppose on the other hand, we had 16 farms, each with just one plot, and eight were selected for trying out the "treatment", with the remaining farms forming the "controls". The analysis then involves the comparison of two independent samples.
It is important to recognise the structure in the data when conducting the analysis. As an example, we show below what is often lost if truly paired results are treated like independent samples. Here the x- and y-values represent the tensile strength of rubber samples collected from two plantations X and Y, on 10 occasions. The aim was to see whether the two plantations differed in the quality of their rubber samples.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Mean | S.D. |
| X(i) | 174 | 191 | 186 | 199 | 190 | 172 | 182 | 184 | 200 | 177 | 185.5 | 9.687 |
| y(i) | 171 | 189 | 183 | 198 | 187 | 172 | 179 | 183 | 199 | 176 | 183.7 | 9.764 |
| d(i) | 3 | 2 | 3 | 1 | 3 | 0 | 3 | 1 | 1 | 1 | 1.8 | 1.135 |
The difference in the two means is 1.8. For the unpaired analysis the standard error of this difference is calculated using the standard deviations in the last column, and found to be 4.3, leading to a non-significant t-value of 0.41. The correct strategy of a paired analysis uses the differences in the table above. The standard error of these differences is 0.36, leading to a highly significant t-value of 5.0.
The reason for the difference is that in the unpaired analysis, the occasion-to-occasion variation in the samples is included in the calculation of the standard deviations used in the two-sample t-test. Not eliminating this variability means the small but systematic differences between the pairs are not detected. The unpaired analysis is unnecessarily weak where true and effective pairing exists. In general this paired structure is similar to the idea of blocking in experiments and stratification in surveys, and needs to be properly accounted for in any subsequent data analysis.
[TOP]
6. Sample Size
One common question that is posed to statisticians is how large a sample is needed. To be able to answer this type of question for an experiment or survey, information must be given on (1) how small a difference is it important to detect, and (2) how variable will the observations be for the key response(s) of interest. This variability is usually reflected in the residual standard deviation of the data, because it is the unexplained variation of the data that relates to the precision of our data.
These two elements are needed for the sample size to be evaluated, otherwise a statistician could not be expected to rubber-stamp the corresponding study as being adequately planned to achieve a formal objective. This does not deny the importance of exploratory or pilot-studies, where the aim is to generate or specify hypotheses, or to evaluate a proposed methodology for the future.
One reason for considering hypothesis tests is that their simplicity provides a basis for the evaluation of many sample size calculations. This involves the power of the test, i.e. the probability of correctly rejecting the null hypothesis when it is false. If your sample size is sufficient, then you will have a high power to detect a difference that you regard as being important.
Modern statistical packages, such as Minitab, incorporate extensive facilities for sample size or power calculation. There are also specialist packages, such as nQuery. It is probably easier to improve ones "feel" for power or sample size calculations through hands-on use of a package than from a demonstration.
As an example we take the paired t-test considered in Section 5.3. Suppose that our aim is to choose the sample size, i.e. how many samples we need for a similar study. We suppose that the value of s will be about the same as before, that is about 1.1 and that we would like to detect a mean difference in tensile strength of rubber between the two plantations, of more than 1 unit with probability 0.95, i.e. we look for a power of 0.95. Further, we suppose the test is to be conducted at the 5% level. Putting these conditions into Minitab gives a required sample size of 18 units.
If this is too many and we can only have 10 observations, we can keep our difference of 1 unit and we would find that the power is 0.73. Or we can ask for what difference the power will be 0.95, giving a value of a mean difference of 1.4. These results can then provide a basis for a discussion on the appropriate study to be conducted.
A study whose power is low may have little ability to discern meaningful results. It should be reconsidered, so it is large enough to establish important effects, or abandoned if it cannot be expected to do so. Too large a study wastes resources, while one that is too small tends also to be wasteful, as such studies often result in inconclusive findings. Study size calculations are usually closely related to decisions on expending resources, so it is important to get them right.
The choice of values for the power and significance levels in sample size calculation is debatable. Setting the significance level at the conventional values of 5% or 1%, quantify the probability of falsely rejecting the null hypothesis, when it is true. This is known as a Type I error. The power to detect a minimum meaningful difference, if it exists, quantifies a second type of error, conventionally called a Type II error, namely that a real difference will remain undetected. Commonly sample size calculations specify a power of 80%, though 90% is also used.
When using results such as the example above it is important to remember that the calculations of sample size or power relate to a single hypothesis. Most studies have a number of objectives and significance testing is usually only a small part of the analysis. In general the same type of calculation should therefore be done for a number of the key analyses to ensure that the sample size is sufficient for all the objectives of the study. Thus the proper planning of a data collection study requires that the main analyses are foreseen and planned for, before the data collection is allowed to start.
[TOP]
7. Non-Parametric Methods
The normally distributed measurement is the starting point of much statistical analysis. There are situations where this seems worryingly inappropriate. Measurements are perhaps from a very skew distribution, where an occasional reading is much larger than the usual range and cannot be explained or discounted. Results may be only quasi-numerical, e.g. an importance score between 1 and 10 allocated to several possible reasons for post-harvest fish losses. Different fishermen may assign scores in their own way, some avoiding extreme scores, while others using them. We may then have reasonable assurance as to the rank order of scores given by each individual, but doubtful about applying processes such as averaging or calculating variances for scores given to each reason.
In
such cases it is sensible to consider using non-parametric methods.
A simple example is the paired data shown earlier in Section
5.1. Here the ten differences in breaking strength were as follows:
3 2 3 1 3 0 3 1 1 1
Earlier we used the t-test, but a simple non-parametric test
follows from the fact that nine out of the ten values are positive,
with the other being zero. If there were no difference in the before
and after reading we would expect about half to be positive and
half negative, so this simple summary of the data provides good
evidence (p = 0.004, on a formal test) against this hypothesis.
Just noting whether the observations are positive, zero or negative
is also clearly robust against occasional readings being very large
- if the first difference were 30, rather than 3, this would not
affect the analysis. Thus non-parametric methods often provide a
simple first step. They also add easily explained support for the
conclusions from a parametric analysis.
We advise caution, however, about the over-use of non-parametric methods. Inadequate understanding of the data-generating system by the researcher may be the real reason for messy-looking data. A common reason for apparently extreme values, or lumpy distribution of data, is often that the population sampled has been taken as homogeneous, when it is an aggregate of different strata, within which the observations follow different patterns.
Sometimes problem data arise from poorly designed measurement procedures, where a more thoughtful definition of raters' tasks would produce more reliable data. It is then better to think harder about the structure of the data than to suppress the complications and use an analysis that ignores them.
The ethos of non-parametric methods often stems from assuming the measurements themselves are flawed, or at least weak, so that estimation procedures are of secondary importance. The primary focus of most non-parametric methods is on forms of hypothesis testing, whereas the provision of reasonable estimates usually generates more meaningful and useful results.
In the final section of this guide we outline a more general framework for the analysis of many sets of data that used previously to be processed using non-parametric methods.
[TOP]
8. Analysis of Variance
8.1 Introduction
8.2 One-Way ANOVA
8.1 Introduction
Practical problems are usually more complicated than the illustrations so far. We use the Analysis of Variance to illustrate how the concepts are applied in larger problems.
Understanding the idea of analysis of variance is now a more general requirement than just to analyse experimental data. The same type of generalisation is possible for data on proportions, or where regression, or time-series methods would be used. When data are from non-normal distributions, such as survey data on counts, then the ideas of Analysis of Variance are generalised and are then called the Analysis of Deviance. The key concepts remain unchanged.
8.2 One-Way ANOVA
The t-test for two independent samples shown in Section 5 generalises to more than two samples in the form of the one-way analysis of variance. The comparison of a collection of independent samples is described as a "completely randomised design". We illustrate this with an example.
In
a study of species diversity in four African lakes the following
data were collected on the number of different species caught in
six catches from each lake.
| Lake | Tanganyika | Victoria | Malawi | Chilwa |
| Catch 1 | 64 | 78 | 75 | 55 |
| Catch 2 | 72 | 91 | 93 | 66 |
| Catch 3 | 68 | 97 | 78 | 49 |
| Catch 4 | 77 | 82 | 71 | 64 |
| Catch 5 | 56 | 85 | 63 | 70 |
| Catch 6 | 95 | 77 | 76 | 68 |
| Mean | 72 | 85 | 76 | 62 |
The pooled estimate of variance, 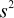 ,
is 100.9. The standard error of the difference between any two of
the above means is
,
is 100.9. The standard error of the difference between any two of
the above means is
.
The
usual analysis of variance (ANOVA) will look like:
One-way
ANOVA: catch versus lake
Analysis
of Variance for catch
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
The F-value and p-value are analogous to the t-value and p-value in the t-test for two independent samples. Indeed, the two-sample case is a special case of the one-way ANOVA, and the significance level is the same, irrespective of which test is used.
With more than two groups a significant F-value, as here, indicates there is a difference somewhere amongst the groups considered, but does not say where - it is not an end-result of a scientific investigation. The analysis then usually continues with an examination of the treatment means that are shown with the data above. Almost always a sensible analysis will look also at "contrasts" whose form depends on the objectives of the study. For example if lakes in the Tanzanian sector were to be compared with the Malawian lakes, we could look at the difference in the mean of the first two treatments, compared with the mean of the third and fourth. If this difference were statistically significant, then the magnitude of this difference, with its standard error, would be discussed in the reporting the results.
In the analysis of variance a "non-significant" F-value may indicate there is no effect. Care must be taken that the overall F-value does not conceal one or more individual significant differences "diluted" by several not-very-different groups. This is not a serious problem; the solution is to avoid being too simplistic in the interpretation. Thus again researchers should avoid undue dependence on an arbitrary "cut-off" p-value, like 5%.
8.3 Multiple Comparison Tests
These tests are often known by their author and include Dunnett's test, Neumann Keuls, etc. They concern the methods of testing differences between means, which require ANOVA type analyses. Some scientists use them routinely while others avoid their use.
Our views are perhaps clear from Section 5.2. Hypothesis testing is usually just a preliminary step, and the further analysis, often concerning the treatment means, relates directly to the stated objectives of the study. This will usually involve particular contrasts, to investigate differences of importance. We do not recommend multiple comparison methods, because they usually do not relate to the objectives of the research.
The case for the multiple comparison tests rests on the danger of conducting many significance tests on a set of means, for example comparing the largest with the smallest, without adjusting the test for the fact that we have deliberately chosen them as being largest and smallest. The case is clear, but irrelevant to us in most analyses, because we do not wish to do lots of tests. We want, instead to investigate the size of differences in relation to their practical importance.
To take one field of application, that of agricultural field trials, then usually the treatment structure will be well defined, with factorial structure being the most common. In such cases multiple comparison procedures are usually clearly not relevant. The only type of factor where we might wish to consider multiple comparison methods would be perhaps variety comparison (of maize, say) where we might wish to present the results in descending order of the mean yields. Even here, we are more likely to try and understand the differences in yields as a function of the season length, or country of origin, etc of the varieties, than to suggest a series of tests. The one case for the tests would be if we wish to group the varieties into sets that behave similarly. Some might use multiple comparison methods for this. We would suggest cluster analysis, which has the additional advantage that it can be used on many variables together. Even here, we would suggest that the cluster analysis should usually be part of a preliminary study, to be followed by attempts to understand the reasons for varieties being in one cluster or another.
Our main concern is that users may be tempted to use a multiple comparison method instead of a more thoughtful analysis, and hence will miss interpreting the data in ways that are needed given the objectives of the study. As long as you do not fall into this trap, then we invite you to do both. We predict that when you report the results in relation to the objectives, you will not need to use any of the results from the multiple comparison methods. So they can then be deleted from the tables in the report!
We also discuss this problem in the guide on Informative Presentation of Graphs, Tables and Statistics because some scientists may have withdrawal symptoms if they do not present tables with a collection of letters beside the corresponding means.
[TOP]
9. A General Framework
The illustrative examples in this guide have all been simple, to concentrate on the concepts. These concepts include:
- Our data are (or are assumed to be) a sample from some population, and we wish to make inferences about the population.
- We therefore use our sample to estimate the properties (parameters) of the population that correspond to the objectives of our study.
- The standard error of the estimate is its measure of precision. Sometimes we report the standard error itself and sometimes we report a confidence interval for the unknown parameter.
- We often use hypothesis (significance) tests to identify whether differences between parameters can be detected in our study. This testing phase is often the first step in the inference part of the analysis.
All the examples in this guide can be written in a general way as:
data = pattern (or model) + residual
This is our assumed model for the population. For example, the problem of strength of rubber can be written as:
Strength = Occasion effect + Plantation effect + residual
Our objective was to investigate the difference between the two plantations, and the effect was clear. But we also saw in Section 6, that if we omitted the occasion effect from the model, i.e. if we used the simpler model:
Strength = Plantation effect + residual
then we could not detect the Plantation effect. This showed that we need the "Occasion effect" in the model, even though studying the size of the Occasion effect might not have been one of our objectives.
The model above is the same if there are more than two plantations, as in Section 7 and would still apply if the data were not "balanced", i.e. if plantations did not send samples on all occasions. With standard statistics packages the inferences can still be made.
Earlier, one limitation was that the data had to come from a distribution that was approximately normal, but this is no longer the case. Parametric methods are now very flexible in dealing with well-behaved data, even when not normally distributed and this often provides an attractive framework for data analysis than the simple tests that are often still in current use. For example, instead of using a simple chi-square test to examine relationships in a two-way contingency table, the use of log-linear models provides a more general and usable framework, for inferences about proportions. This general framework can be used with both two-way tables (like a chi-square test) and with more complicated tables of counts.
Within this general context, significance tests are often used to provide guidance on how complicated a model is required. Then, using the chosen model, we estimate, as above, the properties that correspond to our objectives, and give a measure of precision to indicate our level of confidence in reporting the results.
Last updated 14/04/03