Modern Methods of Analysis
Release date: March 2001
This is one of a series of guides for research and support staff involved in natural resources projects. The subject-matter here is advanced methods of analysis, including log-linear modelling, logistic regression and multivariate methods. Other guides give information on allied topics.
Contents
- Introduction
- Linking standard methods to modern methods
- Exploratory Methods
- Multivariate methods
- Generalised Linear Models
- Multilevel Models
- In Conclusion
1. Introduction
This is the third guide concerned with the analysis of research data. The ideas apply whatever the method of data collection. They extend the methods described in the basic guides titled Approaches to the Analysis of Survey Data and Modern Approaches to the Analysis of Experimental Data.
The previous guides were both concerned with methods of analysis that researchers should be able to handle themselves. They showed that a large proportion of the analyses often only involved descriptive methods. But research studies do normally include some elements of generalising from the sampled data to a larger population. This generalisation requires the notions of "statistical inference", which are described in the guide Confidence & Significance: Key Concepts of Inferential Statistics.
We first distinguish between " the modern approaches" that are outlined in the basic guides and the "modern methods" that we describe here. The former consist mainly of methods that were already available in pre-computer days. Some were not easy to apply without running into computational difficulties. Current computing software has taken away the strain and the methods can now be used easily.
The methods described in this guide are technically more advanced and are not practical without modern computer software. They are rarely applied in non-statistical research. We describe the most important of these methods and illustrate their use. Our aim is to permit users to assess whether any of these method would be of value for their analysis.
We concentrate on four areas. These are: modern exploratory tools applicable at initial stages of the analysis, descriptive multivariate techniques, extensions of regression modelling to generalised linear models, and multilevel modelling techniques.
2. Linking standard methods to modern methods
The major advances that have simplified many statistical analyses are in providing a unified framework that generalises the ideas of simple regression modelling. Regression is typically thought of as the modelling of a normally distributed measurement, such as crop yield, on a number of explanatory (x) variables, such as the amount of fertilizer, number of days spent weeding, amount of rainfall during crop growth, etc. An alternative approach is to apply the analysis of variance technique, for comparing say different tree thinning methods in a forestry trial, where again, the response variable (e.g. tree height) would be assumed to have a normal distribution.
The first part of the unified approach (as described in Modern Approaches to the Analysis of Experimental Data) is that regression models can easily handle both situations above. In this first stage of generalization we still assume normality for the response variable but the explanatory variables may be a mixture of both factors (classification variables) and variates (numerically measured variables).
If the data were not normally distributed, but were still quantitative measurements such as the percentage of plants that germinated or the number of plants of the parasitic weed Striga in a plot, then the traditional approach is to transform the data before analysis. Such transformations are usually no longer necessary because it is possible to model the data as they are, taking account of the actual distributional pattern of the data. In the case of plant germination, the percentages can be often be thought of as arising from binomial data (yes/no for germination) or following a Poisson distribution as in the case of Striga plant counts. This leads to what are called Generalised Linear Models, described in Section 5.
If the data are qualitative, like adopting a new technology, or not, the traditional approach used chi-square tests to explore how adoption is related to other socio-economic variables taken one at a time. Chi-square tests are limited in terms of being restricted to just two categorical variables. There is also no concept of one of the two variables being dependent on the other.
An extension of the chi-square test leads to another special case within the generalised linear modelling framework. This is the use of log-linear models, to study how a group of categorical variables are associated with each other. Here, the cells of the multi-dimensional table are modelled. This allows the inter-relationships among all the categorical variables to be taken into account in the analysis. These may be ordered responses, such as very good, good, average, poor, very poor, in which case the analysis is called "the analysis of ordered categorical data", or they may be nominal, such as the main reasons for non-adoption of a technology.
The second type of generalisation to consider is that of modelling data that is at multiple levels. In special circumstances, standard analysis of variance methods can also be used, examples being split plot designs or lattices. These involve more than one error term to incorporate variation at the different levels. On-farm trials and surveys also often have information at multiple levels, for example village, farms within village, plots within farms, but these have been more difficult to analyse in the past because the data are often unbalanced. The more general framework, described in Section 6, involves the use of multilevel modelling, to deal appropriately with data which occurs at several levels of a hierarchy.
The main risk with the availability of general modelling approaches is that they will be used for complex data sets without the analyst looking at the data first. Thankfully exploratory methods have also advanced; trellis plots, multiple boxplots, etc. have become available. We therefore start this guide by looking at ideas of exploratory methods. Multivariate methods can also be useful at the exploratory stage and we describe possible roles for principal component and cluster analysis procedures in Section 4.
3. Exploratory Methods
The value of data exploration has been emphasised in earlier guides. However, many exploratory methods are graphical and simple graphs can cease to be of value if the data sets are large. There is then a risk that users omit this stage, because they can see little from the simple forms of data exploration that are suggested in text books. Graphical methods also lose much of their appeal, as exploratory tools, if users need to devote a lot of time to prepare each graph. We look here at examples that are easy to produce, and that can take account of the structure to the data, for example an experiment may be repeated over four sites and six years. A survey may be conducted within seven agro-ecological zones in each of three regions. Looking at such data lends itself to the generation of a "trellis plot", which allows a simple graphical display to be shown for each of several sub-divisions of the data. This is useful because it is usually easier to look at a lot of small graphs together (than several separate graphs) to obtain an overview of inter-relationships between key variables.
Similarly there are other types of plot, one called a scatterplot matrix that enable us to look at many variables together, while distinguishing between different groups, i.e. to look at aspects of the structure, within each plot. In some software, these graphs are "live", in the sense that you can click on interesting points in one graph and then have some further information. This may be to see the details of those points, or see where related points figure in other plots. The main message is not to allow yourself to be overwhelmed by large datasets. They are harder to handle, but that means being more imaginative in how you examine the data, rather than avoiding this stage.
Figures 1 and 2 give examples of exploratory plots. The first shows multiple boxplots to demonstrate the effect on barley yields to increasing levels of nitrogen (N) at several sites (Ibitin, Mariamine, Hobar, Breda, Jifr Marsow) in Syria. In addition to demonstrating how yields vary across N levels and how the yield-N relationship varies across sites, individual boxplots show the variation in yields for a constant N application at a particular site and highlights the occurrence of outliers (open circle) and extremes (*).
Figure 1. Multiple boxplots for barley yield response to nitrogen
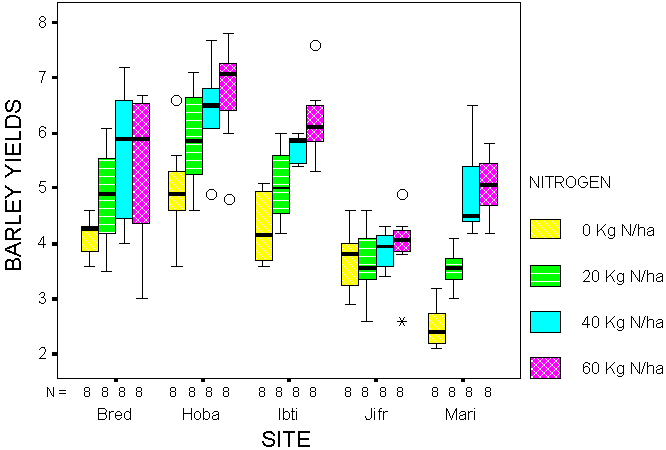
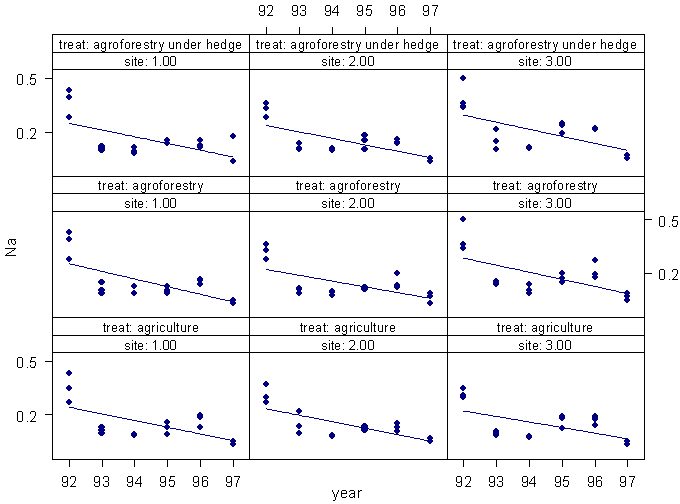
This graph is as complex as one would want and perhaps would be clearer if split into separate graphs for each site. Figure 2 shows a typical example of a trellis plot, for the variation in soil measurements (Na is used for illustration) over several years, shown separately at three sites for each of three separate treatments. (The actual study was a 5 × 5, but has been cut down for this illustration).
Figure 2. Sodium (mmeq/100g) in soil plotted by years, separately
for each of three sites and three treatments
4. Multivariate methods
4.1 Cluster Analysis
4.2 Principal Component Analysis
Researchers are sometimes concerned that they cannot be exploiting their data fully, because they have not used any "multivariate methods". We distinguish here between methods such as principal component analysis, which we consider as multivariate, and multiple regression analysis, which we consider to be univariate.
The distinguishing feature is that in a multiple regression analysis we have a single (univariate) y of interest, such as yield or the number of months per year when maize from home garden is available for consumption. We may well have multiple explanatory x's, e.g. size of home garden, labour availability, etc., but the primary interest is in the single y response.
We may need multivariate methods if for example we want to look simultaneously at intended uses of tree species such as y1=growth rate, y2=survival rate, y3=biomass, y4=degree of resistance to drought, and y5=degree of resistance to pest damage. The simultaneous study of y1, y2, y3, y4 and y5 will help more than the separate analysis if the y variables are correlated with each other. So a large part of multivariate methods involves looking at inter-correlations.
It should be noted that it is also perfectly valid and often sufficient to look at a whole series of important y variables in turn and this then constitutes a series of univariate analyses.
Studies sometimes begin with univariate studies and then conclude with a multivariate approach. This is rarely appropriate. Instead we suggest that the most common uses of multivariate methods are as exploratory tools to help you to find hidden structure in your data. Two common methods are principal component analysis and cluster analysis. We outline the roles of these two methods, so you can assess whether they may help in your analyses.
4.1 Cluster Analysis
Consider a baseline survey which has recorded a large number of variables, say 50, on each of 200 farmers in a particular region. Assume most of the variables are categorical and a few are numerical measurements.
Suppose that an on-farm trial was used with these farmers to compare a number of weed management strategies (call these treatments), and gave results that demonstrated a farm by treatment interaction, i.e. not all farmers benefit by the same management strategy. We now want to explore reasons for this interaction. One method may be to investigate whether particular strategies can be recommended for groups of farmers who are similar in terms of their socio-economic characteristics. A first step then is to group the farmers according to their known background variables and this is the part that is multivariate.
Cluster analysis tries to find a natural grouping of the units under consideration, here the 200 farmers, into a number of clusters on the basis of the information available on each of the farmers. The idea is that most people within a group are similar, i.e. they had similar measurements. It would simplify the interpretation and reporting of your data, if you found that the 200 farmers divided neatly into four groups and that farmers within each group had similar responses with respect to the effectiveness of the weed management strategies. The four groups then become the recommendation domains for the weed management strategies.
Cluster analysis is a two-step process. The first step is to find a measure of similarity (or dissimilarity) between the respondents. For example, if the 50 variables are Yes/No answers, then an obvious measure of similarity between 2 respondents is the number of times that they gave the same answer (see illustration below). If the variables are of different types, or on different themes, then the construction of a suitable measure needs more care. In such cases, it may be better to do a number of different cluster analyses, each time considering variables that are of the same type, and then seeing whether the different sets of clusters are similar.
Once a measure of similarity has been produced, the second step is to decide how the clusters are to be formed. A simple procedure is to use a hierarchic technique where we start with the individual farms, i.e. clusters of size 1. The closest clusters are then gradually merged until finally all farms are in a single group. Pictorially this can be represented in the dendogram shown in Figure 3. In this example, if three clusters could be formed, made up of the sets (1), (7) and (2,3,4,5,6,8); or 5 clusters made up of (1), (7), (4,5,8), (2,3) and (6), and so on. This is obtained by drawing a line at different heights in the dendogram and selecting all units below each intersected line.
If you use this type of method, do not spend too long asking for a "test" to determine which is the "right" height at which to make the groups. Remember cluster analysis is just descriptive statistics.
As an example, consider the data in Table 1 from eight farms, extracted from a preliminary study involving 83 farmers in an on-farm research programme. The variables were recorded as 'Yes' (+) and 'No' (() on characteristics determined during a visit to each farm. The objective was to investigate whether the farms form a homogeneous group or whether there is evidence that the farms can be classified into several groups on the basis of these characteristics.
For this data a similarity matrix can be calculated by counting
the number of +'s in common, arguing that the presence of a particular
characteristic in two farms show greater similarity between those
two farms than the absence of that characteristic in both. The matrix
of similarities between the eight farms appears in Table 2. This
is useful to study in its own right. For example, you can see that
farms 4 and 8 are the closest because they had 6 answers in common.
The dendogram in Figure 3 was produced on
the basis of these similarities.
Table 1. Farm data showing the presence or absence of a range of farm characteristics.
| Farm (Farmer) | ||||||||
| Characteristics | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Upland (+)/Lowland (-)? | - | + | + | + | + | + | - | + |
| High rainfall? | - | + | + | + | + | - | - | + |
| High income? | - | + | + | - | - | + | - | - |
| Large household (>10 members)? | - | + | + | + | - | + | - | + |
| Access to firewood within 2 km? | + | - | - | + | + | - | + | + |
| Health facilities within 10 km? | + | - | - | - | - | - | - | - |
| Female headed? | + | - | - | - | - | - | - | - |
| Piped water? | - | - | - | - | - | - | + | - |
| Latrines present on-farm? | + | - | - | - | - | + | - | - |
| Grows maize? | + | - | - | + | + | - | + | + |
| Grows pigeonpea? | - | + | + | + | - | + | - | - |
| Grows beans? | - | - | - | + | + | - | - | + |
| Grows groundnut? | - | - | - | - | - | - | - | + |
| Grows sorghum? | + | - | - | - | - | - | - | - |
| Has livestock? | + | + | - | - | + | - | + | - |
Table 2. Matrix of similarities between eight farms (cf. Figure 3)
| Farm | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | - | 1 | 0 | 2 | 3 | 1 | 3 | 2 | |
| 2 | - | 5 | 4 | 3 | 4 | 1 | 3 | ||
| 3 | - | 4 | 2 | 4 | 0 | 3 | |||
| Farm | 4 | - | 5 | 3 | 2 | 6 | |||
| 5 | - | 1 | 3 | 5 | |||||
| 6 | - | 0 | 2 | ||||||
| 7 | - | 2 | |||||||
| 8 | - | ||||||||
Figure 3. Dendogram formed by the "between farms" similarity matrix.

4.2 Principal Component Analysis
Suppose that in the example used initially in 4.1, many of your 50 measurements are inter-correlated. Then you don't really have 50 pieces of information. It may be much less. Could you find one or more linear combinations (like the total from all the numerical measurements), that explain as much as possible of the variation in the data? The linear combination that explains the maximum amount of variation is called the first principal component. Then you could find a second component, that is independent of the first and that explains as much as possible of the variability that is now left. Suppose you find 3 linear components that together explain 90% of the variation in your data. You have then essentially reduced the number of variables that you need to analyse from 50 down to 3!
If you put these ideas concerning cluster analysis and principal component analysis together, then you have reduced your original data of 200 farmers by 50 measurements down to 4 clusters by 3 components. You can then write your report, which is much more concise than it could possibly have been without these methods.
This may seem wonderful. So where are the catches? Well the main catch is that very few real sets of data would give a clear set of clusters or as few as three principal components explaining 90% of the variation in the data. Often, there may be additional structure in the data that was not used in the analysis.
For example, the data may have come from a survey in 6 villages, in which half the respondents in each village were tenant farmers. The remainder owned their land. This information represents potential groups within the data, but were not included in the cluster analysis. Hence often the cluster analysis will rediscover structure that is well known, but was not used in the analysis. It is sometimes valuable to find that the structure of the study is confirmed by the data, i.e. people within the same village are more similar than people in different villages. But that is rarely a key point in the analysis.
This problem affects principal components in a similar way, because a lot of the variation in the data may be due to the known structure, which has been ignored in the calculation of the correlations that are used in finding the principal components. Another major difficulty with principal component analysis is the need to give a sensible interpretation to each of the components which summarise the data. An illustration is provided below to demonstrate how this may be done, but the answer is not always obvious!
Pomeroy et al (1997) describe a study where 200 respondents were asked to score a number of indicators, on a 1-15 scale, that would show the impact of community-based coastal resource management projects in their area. The indicators were:
| 1. Overall well-being of household | 6. Ability to participate in community affairs |
| 2. Overall well-being of the fisheries resources | 7. Ability to influence community affairs |
| 3. Local income | 8. Community conflict |
| 4. Access to fisheries resources | 9. Community compliance and resource management |
| 5. Control of resources | 10. Amount of traditionally harvested resource in water. |
These 10 indicators were subjected to a principal component analysis to see whether they could be reduced to a smaller number for further analysis. The results are given in Table 4 for the first three principal components.
Table 4. Results of a principal component analysis
| Component | |||
|
Variable | PC1 | PC2 | PC3 |
| 1. Household | 0.24 | 0.11 | 0.90 |
| 2. Resource | 0.39 | 0.63 | 0.02 |
| 3. Income | 0.34 | 0.51 | 0.55 |
| 4. Access | -0.25 | 0.72 | 0.17 |
| 5. Control | 0.57 | 0.40 | 0.12 |
| 6. Participation | 0.77 | 0.13 | 0.29 |
| 7. Influence | 0.75 | 0.22 | 0.34 |
| 8. Conflict | 0.78 | 0.03 | 0.18 |
| 9. Compliance | 0.82 | 0.12 | 0.07 |
| 10. Harvest | 0.38 | 0.66 | 0.12 |
| Variance % | 33 | 19 | 14 |
Thus component 1 (PC1) is given by:
PC1 = 0.82(Compliance) +0.78(Conflict) +0.77(Participation) + ... +0.24(Household).
By studying the coefficients corresponding to each of the 10 indicators, the three components may perhaps be interpreted as giving the following new set of composite indicators.
PC1 : an indicator dealing with the community variables;
PC2 : an indicator relating to the fisheries resources;
PC3 : an indicator relating to household well-being.
These summary measures may then be further simplified. For example, if we were planning to take the total score in variables 6 to 9 as an indicator of compliance, then principal component analysis might re-enforce that this first principal component could be a useful summary for this set of data. We discuss indicators in the Approaches to the Analysis of Survey Data guide.
Finally, we repeat our general view that where multivariate methods are used, their main role is often at the start of the analysis. They are part of the exploratory toolkit that can help the analyst to look for hidden structure in their data.
[TOP]
5. Generalised Linear Models
In many studies some of the objectives involve finding variables that affect the key measurements that have been taken. Example of key measurements are:
* crop yield
* number of weeds
* adoption (yes/no) of a suggested technology
* success or otherwise of a project promoting co-management of non-timber forest products
* level of exploitation of fisheries resources in a community (none/low/medium/high).
In the case of the first three variables above, one objective may be to study the extent to which these measurements, say the crop yields, are related to the amount of fertilizer application, availability of credit, level of education, and so on. With the latter variables, an objective may be to determine how, say the chance of success, is affected by income, participation in community activities, interest in the welfare of the community as a whole, ability to solve community conflicts, etc.
Generalised linear models extend the regression ideas to develop similar types of model for measurements (like the number of weeds or a yes/no response) that are not necessarily normally distributed. Various examples have been available for a long time, one is called "probit analysis". What we now have is a general framework within which this is just one example.
Dealing with counts data, like the number of weeds, leads to Poisson regression models; while data in the form of a yes/no response, or a proportion (e.g. proportion of seeds germinating) use logistic (or probit) regression models. When the key measurement is a categorical response involving more than two categories, e.g. low/medium/high, the data can be modelled using log-linear modelling techniques.
A common feature of all these models is that they involve a data transformation and a specific distribution describing its variability. They all fall within the class of generalised linear models. The advance, stemming from a key paper in 1972, was to consider all problems concerning different types of data in a unified way, and to produce computer software that could conduct the analyses. This software was produced by the Rothamsted Experimental Station and was called GLIM (Generalised Linear Interactive Models). The methods are now sufficiently well accepted to be available in most standard statistics packages. A more recent advance has been the ease of use of these packages. This has put these methods easily within the reach of non-statisticians.
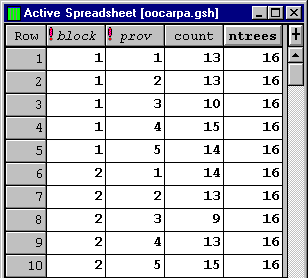
As a simple illustration consider data from a randomised complete block design, with two blocks, to compare the performance of five provenances of the Ocote Pine, Pinus oocarpa. One variable of interest was the number of trees, out of a possible 16, which were still surviving after 7 years. The data are shown in Figure 4.
Figure 4. Part of the data from a provenance trial
In the guide Modern Approaches to the Analysis of Experimental Data, we noted that the essentials of a model are described by
data = pattern + residual
e.g. yield = constant + block effect + variety effect + residual.
When the left hand side consists of proportions which estimate (say in the example above) the probability p ij of survival of provenance j in block i, the corresponding generalised linear model becomes
i.e. log(p ij/(1-p ij)) = constant + block effect + provenance effect
More conveniently we can write
logit p ij = constant + block effect + provenance effect
where logit p ij = log (p ij / (1 - p ij ) . For the analysis, the counts in Figure 4 above are assumed to follow a binomial distribution.
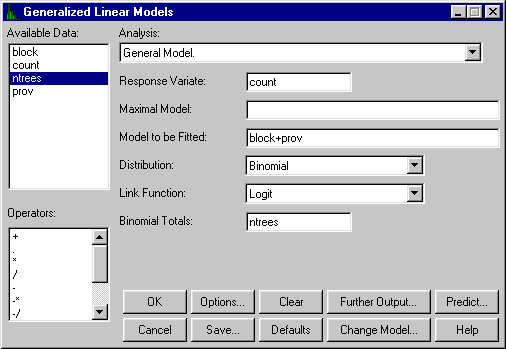
The ease with which the analysis can be done is shown by Figure 5a below, which shows the dialogue that would be used (Genstat is used as illustration here) to analyse data where the response, instead of being a variate like yield, is a yes/no response that arises, for instance, in whether or not a new technique is adopted.
Figure 5a. Dialogue in Genstat to fit a generalised linear model for proportions
The output associated with the fitted model includes an "analysis of deviance" table (see Figure 5b). This is similar to the analysis of variance (anova) table for normally distributed data. The residual deviance is analogous to the residual sum of squares in an anova. In place of the usual F-tests in the anova, chi-square tests are used to assess whether the survival rates differ among the provenance (in other cases, we would use approximate F-tests). Here the p-value gives evidence of a difference.
Figure 5b. Analysis of deviance table for proportion of surviving trees
Change |
|
deviance |
approx |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Estimates for the probability of survival can be obtained via the Predict option in the dialogue box shown in Figure 5a. The results are shown in Figure 5c.
|
Figure 5c. Predicted probabilities on survival for each provenance
When the key response measurement is in the form of counts or proportions or is binary (yes/no type), one advantage in modelling the data to take account of its actual distribution (Poisson, Binomial or Bernoulli) is that the summary information is always within the expected limits. For example the estimate is 0.8437 (or 84%) in Figure 5c for the first provenance. Thus, model predictions for the true proportion of farmers in a community who adopt a recommended technology will be a number between 0 and 1. In traditional methods of analysis, the resulting predictions could well give unrealistic values such as values greater than 1 for proportions data or negative values for counts data. The availability of generalised linear models simplifies and unifies the analysis for many sets of data, and it enables the effect of different explanatory variables and factors to be assessed in just the same way as is done for ordinary regression when responses are normally distributed. However, we do not expect miracles. For example, when analysing yes/no data on adoption, each respondent provides only a small amount of information (yes or no!). Hence a large sample size is needed for an effective study. Our guide Confidence & Significance: Key Concepts of Inferential Statistics discusses sample size issues. Thus, if the sample size is small there is little point in building complicated models for the data. A simple summary, say in terms of a two-way table of counts, may be all that can be done. Log-linear models also fall within the class of generalised linear models. Such models extend the ideas of chi-square tests to more than two categorical variables, thus allowing the simultaneous study of several categorical variables. Here we consider models where the dependence of a categorical variable, such as the main type of agricultural enterprise undertaken by rural households, on a number of explanatory variables is to be investigated. As illustration we consider the working status of male children in a study aimed at exploring factors that may effect this status. The primary response is then Factor Y (say) = working status of the male child (school going/supporting father at work/working in an external establisment) Suppose the following are potential explanatory factors that effect Y. A = location of child's family unit (peri-urban/rural) B = education level of father (low/medium/high) X = number of months the family unit subsists on staple crop grown on own land. Of the above, A and B are categorical variables, while X is quantitative. To apply log-linear modelling techniques, the continuous variable X too is classified as a factor (C say) defined as: C = 1 if X ( 3 months; 2 if 3 < X ( 6 months; 3 if 6 < X ( 12 months. The data structure would then look like that given in Table 5. As with logistic or Poisson regression modelling, analyzing these data via log-linear modelling techniques involves the use of a table of deviances. The dependence of Y on A, B, C and their interactions involves looking at changes in deviances between a baseline model and the alternative model that includes the interaction of Y with each of A, B, C and their interactions. Sample size issues are still a concern when we move to log-linear models. With little data there is not much point in attempting to consider models with many factors because the corresponding cell counts will be very small. The results will be "non-significant" simply because there is insufficient information to differentiate between alternative models. Thus, as with chi-square tests, tables with many zero counts can lead to misleading conclusions.
Table 5. A typical data structure for exploring relationships between categorical variables
6. Multilevel ModelsMany studies involve information at multiple levels. A typical example is a survey, or on-farm trial where some information is collected about villages (agro-ecological conditions), some from households in these villages (family size, male or female headed, level of education of household head) and some on farmers fields (soil measurements, tillage practice, yields). Here there are 3 "levels", namely village, household and field. Often as here, these "levels" are "nested" or "hierarchical", so that the fields are within the households and the households are within the villages. Simple analyses involve separate analyses at each "level", and this approach has been described in the guides Approaches to the Analysis of Survey Data and Modern Approaches to the Analysis of Experimental Data. Here we consider modelling the data, taking account of its hierarchical structure. As with generalised liner models some special cases of multiple levels have been analysed routinely for many years. We consider one such case below. The advance is that we now have a general way of modelling multilevel data. These facilities are currently only available in powerful statistics software. One of the most general packages is called MLwiN. This was developed at the Institute of Education at the University of London and reflects their work in the analysis of data from educational studies that has to consider multiple levels. In particular education innovations were usually taught to whole classes, but most of the data were collected from individual pupils. Other statistics packages with similar facilities to MLwiN include SAS (Proc Mixed) and Genstat (REML). Livestock studies have faced these problems routinely, because there is often data on herds, then on individual animals and then repeated measurements within each animal. One early attempt to provide a computer solution was a package by Harvey, which was recommended by the International Livestock Research Institute (ILRI) for many years. When data are at one level, we emphasised that a model could be formulated roughly as: data = pattern + residual. To explain why this formulation is no longer sufficient one could consider a simple case of a "split plot" experiment, for which the analysis, for balanced data, has been routine, even in pre-computer days. Table 6 shows the structure of a typical Analysis of Variance table for such an experiment. It is drawn from a Farming Systems Integrated Pest Management Project (FSIPM) conducted in Malawi in the Blantyre-Shire Highlands. The study involves a trial with 61 farmers, from two Extension Planning Areas (EPAs) to test pest management strategies within a maize/beans/pigeonpea intercropping system. There were four plots in each farm. Farm data (e.g. land type and socio-economic variables) are at the higher level and plot data (e.g. type of seed dressing, damage assessment, crop yields) are at the lower level. For a model containing just the planning areas, land type and seed dressing, the structure is similar to a split-plot experiment in the following way: * Farms within EPAs are similar to mainplots within blocks, and farmers plots are similar to subplots within the mainplots. * The land type is a feature of the farm while the seed dressing can be viewed like the subplot treatment factor. Table 6. ANOVA to study interactions between treatments and farm level stratification variables
The ANOVA table shows why the simple Data = Pattern + residual is no longer sufficient. Because we have 2 levels we have 2 residuals. We now need to write something like data =(farm level pattern)+(farm level residual)+(plot level pattern)+(plot level residual) The key difference is that we now have to recognise the "residual" term at each level. Our analysis is always based on the idea that the residuals are random effects. Now we have more than one random effect. So our model is a mixture of "patterns" and "residuals". This is called a "mixed model". So the advance is largely the development of general tools for analysing "mixed models". In the example above the analysis would be simple because all farms have four plots. The general approach is equally applicable had the measurements been on the animals in each farm, with different numbers in each farm. A companion guide, with examples, is devoted to the formulation and analysis of mixed models. This is titled Mixed Models in Agriculture, and has been written jointly with ILRI. The new general approach has another feature in addition to the facilities to cope with data from multiple levels simultaneously. This is that any of the terms in the model, not just the lowest level residual, could be random. For example, in a regional trial, the villages might be a random sample, so the results can be generalised to the region. Alternatively villages might be fixed, i.e. purposively selected, perhaps to study disease problems in only the "hot-spots". The general facilities to handle mixed models are relatively recent, even for data, like yields, where normal distributions can be assumed. Further developments to non-normal data also exist but are still the subject of statistics research. We believe that researchers need to know of the existence of these methods and be aware that these should add to, and not usually replace, simpler analyses that are done at each separate level. The value of these more modern techniques is in giving more insights than simpler analyses. Where they do not, it is advisable to stick with simpler approaches that may be easier to explain in reports. [TOP] 7. In ConclusionThe advances described in this guide are important, because they make it simpler for researchers to exploit their data fully. Earlier we could handle data easily from a multilevel study, if they were simple, like a balanced split-plot design. The processing became much more difficult if the data were unbalanced, and this is the case for almost all surveys and many on-farm trials. Now, as described in the last section, this is not the case. Similarly, we have had ANOVA and regression analyses for many years. Thus we knew how to process data, if they could be assumed to be from a normal distribution. Otherwise users often had to consider a variety of options, such as relatively arbitrary transformations, or complete changes to perhaps a chi-square test. This "piece-meal" approach has now been replaced by the facilities to handle generalised linear models, described in Section 5. There are now extensions to generalised mixed models if the data are hierarchical. Until recently it has also been quite difficult to use statistical software for the data analysis, particularly if the analysis was not simple. Each statistics package had its own language, and this required both statistical and computing skills to master. The time needed was such that, statisticians apart, users would not consider learning more than one package. This has also changed. Data can now easily be transferred between packages and it is straightforward to use a variety of statistical software, to a reasonable level, without learning the underlying language. Critics will be quick to point to the dangers of users being able to click their way to an inappropriate analysis much faster than before. While this is true, what is more important are the facilities that are now available for users to develop a model for their data that reflects the structure of their study and enables them to analyse their data in ways that are directly related to their objectives. Previously users were often distracted from their direct needs, of learning how to process their data, by the more pressing need to learn the language of the proposed software. There was much to learn, because of the varied methods that depended on the types of data. In this "new world" we hope that users will find both the statistical ideas and the analysis of their data to be a more satisfying part of their work. We hope this guide has indicated when project objectives and data might benefit from these methods despite the considerable challenge in using them unaided. ReferencesPomeroy, R.S., Pollnac, R.B., Katon, B.M., & Predo, C.D. (1997). Evaluating factors contributing to the success of coastal resource management: the Central Visayas Regional Project-1, Philippines. Ocean & Coastal Management, 36: 97-120. Nelder, J.A. and Wedderburn, R.W.M. (1972) Generalized Linear Models. J.R.Statist.Soc., A, 135, 370-384. Last updated 16/04/03 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||