Appendix E

Variances of linear combinations

Assume a multivariate normal distribution for the vector of observations Y

Y ~ MVN (X, V)

For the fixed effects model

Y = X+ E

we typically assume Y ~ MVN (X,²I)

In the overparameterised model, an estimate of , is given by

and the variance-covariance matrix of this estimator is

D ()	= D (GXTY)
	= GXTD (Y) XGT
	= 2GXT XGT

Interest is only in estimable linear combinations of the vector of parameters . A linear combination c^T, is defined to be estimable if c^T, can be written as some linear function of the mean vector E(Y), i.e., with t a (N x 1)-vector (N the number of observations)

c^T = t^TE(Y) = t^TX

From this definition it follows that c^T, is well defined in the sense that it does not depend on the particular choice of G taken to obtain . Indeed

c^T = t^T X= t^TXGX^TY

and XGX^T is invariant to G (see (3) below).

The variance of an estimable function can then be obtained by

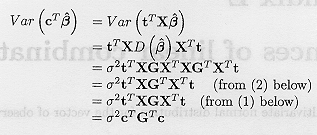
So also the variance of c^T is now independent of the particular choice of G due to the invariance of XGX^T.

Some basic properties of G, the generalised inverse of X^TX, used in the derivation of the variance are

(1) G^T is also a generalised inverse of X^TX
(2) XGX^TX = X
(3) XGX^T is invariant to G. i.e. is the same whatever G.

To provide the reader with some experience in matrix calculations we prove these three statements.

Since G is a generalised inverse of X^TX, it follows that

X^TXGX^TX = X^TX

Taking the transpose gives

(X^TXGX^TX)^T = X^TXG^TX^TX = X^TX

which proves (1).

Starting from (1), we find

X^TXG^TX^TX = X^TX

So

X^TX – X^TXG^TX^TX = 0

This can also be written as (check this by multiplying out)

(X^TXG^TX^T – X^T ) (X^TXG^TX^T – X^T )^T = 0

In general, A^TA = 0 implies A = 0. This can be easily seen by observing that the its` diagonal entry of A^TA is equal to the sum of squares of the elements of the i^th row of A. These diagonal entries can only be zero if A = 0.

If we apply it to our situation, it means that

X^TXG^TX^T = X^T

Taking the transpose gives

XGX^TX = X

which is (2).

To prove (3), suppose that F is another generalised inverse of X^TX. Because of (2)

XGX^TX = X = XFX^TX

Therefore

XGX^TXG^TX^T – XGX^TXF^TXT – XFX^TXG^TX^T + XFX^TXF^TX^T = 0

which can be rewritten as

(XGX^T – XFX^T) (XGX^T – XFX^T) ^T = 0

Because A^TA = 0 implies A = 0, it follows that

XGX^T = XFX^T

which proves (3).