Contents
1. IntroductionThe previous guide discusses research strategy. Research strategy leads to decisions on the choices of studies to undertake. These can be an experiment in a controlled environment, an on-station experiment that cannot be quite as well controlled, an on-farm trial, an observational study that can be cross-sectional (i.e. a set of observations recorded once at one time) or longitudinal (i.e. repeated observations made over time), field testing of an intervention, a survey or a quick ad hoc assessment of the situation in the field, sometimes referred to as a rapid rural appraisal.
This guide discusses the general issues involved in study design. While it is impossible to ignore the particular distinctions between experiments, observational studies, surveys, and so on, as these traditional names are well known, we shall attempt to address study design issues broadly, and attempt to pull together the various design principles, whether they be for an experiment, survey or observational study.
Courses in biometrics often separate the teaching of the design of experiments and the design of surveys. The subjects also tend to be taught in traditional ways. For example, when given an experimental design course, the student may learn about one particular type of design, a randomised block, say, and then another, a Latin Square, maybe, but little time is spent on the general principles of study design that allow the student to design an experiment from scratch.
It might be helpful to prompt some changes in the approach to the teaching of study design and to consider the various "good design" principles together. As research becomes more complicated, there comes a need to design studies that take principles from both surveys and experiments. Furthermore, a project will often involve more than one type of study and often there will be overlaps between studies as one study leads to the next. For example, Case Study 6 shows how different types of studies were used to investigate whether a change in the timing of the feeding of concentrates to dairy cows by providing financial credit to smallholders up front improved lactation yields.
Another example, Case Study 5, describes the various types of studies that need to be undertaken when rationalising 'best bet' accessions (strains) of Napier grass suitable for feeding to livestock in different environments. As already discussed under Research strategy, one of the first tasks for the researcher embarking on a new project is to decide on the most appropriate study needed to address each particular objective.
Sound training is needed, both in the concepts of good study design and in learning how a particular study fits into the overall goals of a research project. This is necessary so that the student knows the appropriate approaches to follow to reach the most suitable design.
An experiment is a study in which a researcher imposes some form of treatment, usually to compare against a control. An experiment aims to provide an answer to a predetermined hypothesis about the perceived effect of a treatment.
An experiment can take place in a controlled environment (e.g. a greenhouse, an animal house or a scientific laboratory). Here variation among experimental subjects can be kept small. Alternatively, an experiment might use experimental land or animals within the facilities of a research institute. Such an experiment is often described as an on-station experiment. Here there will be more variation among experimental subjects and so more care is needed in designing a suitable study.
Case Study 3 and Case Study 4 provide an example of an on-station experiment and deal with data collected from a study designed to compare the performance of different breeds of sheep exposed to helminthiasis in Kenya. Several years were needed to collect sufficient data to account for the variation among animals and to meet the experiment's objectives. Case Study 5 includes a randomised block field experiment to compare characteristics of different Napier grass accessions - another example of an on-station trial. Case Study 15 and Case Study 16 provide two examples of randomised block field factorial experiments designed to compare qualities of dry bean and taro varieties, respectively.
In contrast, Case Study 8 and Case Study 13 are examples of experiments in which animals were kept in individual pens in order to better control environmental error variation. Case Study 9, which investigates optimum conditions for pollen grain germination of the leguminous tree species Sesbania sesban (L.) Merr, is an example of a controlled experiment conducted in a laboratory.
Experiments can also be undertaken 'on-farm' or indeed be laid out across farms (see Case Study 6). These studies are more difficult to manage and the experimental variation is greater. Their advantage, however, is that they match better the real life situation.
Sometimes experiments (for example, Case Study 10, a field study to investigate the impact of an intervention on bovine trypanosomosis) run over time, and measurements are taken on different occasions from the same plots, animals or farms. These experiments involve the concept of different levels of experimental error with variation expressed both among and within experimental units or subjects.
A survey provides a different form of study, one where there is no intervention on the part of the researcher. Although surveys may set out to determine different characteristics among households, for instance, these characteristics or attributes are not imposed in the way that a treatment is imposed in an experiment.
Surveys may have various goals. Case Study 11 and Case Study 12, for example, describe results of a livestock breed survey in Swaziland, designed not only to describe the factors that affect livestock production but also to determine population estimates of numbers of heads of different breeds of livestock and their distributions within the country.
Others may have more simple aims. Thus, Case Study 1 describes a pilot household survey to describe cattle keeping practices of village Orma people in the Tana Delta region of Kenya, and to estimate levels of milk production and utilisation.
An observational study falls in between a survey and an experiment. The researcher observes, as in a survey, but has more control, as in an experiment, on what is done. Sometimes an experiment may be unethical and it may be better to resort to an observational study of relationships between diseased and healthy subjects in the field. Sometimes it is just impossible to simulate by experiment the real life situation.
Case Study 2 provides an example of an observational study and describes how Ankole cattle were monitored in village herds in Uganda in order to identify the highest yielding cattle that might be available for a possible future breeding scheme. Case study14 is another example of an observational study in which factors affecting prevalence of schistosomiasis along a river in Uganda are examined.
On the other hand, Case Study 6 was planned as an across-farm experiment with some farmers assigned to an alternative feeding regime for their cows whilst others continued to apply their existing feeding regimes. However, once control farmers had learnt what other farmers were doing and followed suit, the study collapsed and became a form of observational study.
Case Study 10 describes a tsetse control intervention in Ethiopia superimposed on an existing baseline herd performance and disease prevalence monitoring scheme. This observational study falls under the category of an intervention field-testing study. Such studies often require an earlier period of monitoring to collect baseline data, as was the case here, against which the impact of a subsequent intervention can be assessed.
Case Study 7 is a little different in that it uses previous, routinely-collected meteorological data to examine whether recent declines in crop production in Zambia may be due to possible changes in rainfall patterns. This does not fall strictly into the category of an observational study itself, but nevertheless provides an example of how sets of monitored data can be used to provide answers to research questions without the need to embark on a new study.
A rapid rural appraisal is another form of study technique that has become popular. As the name sounds, it provides a rapid analysis of the situation on the ground through interviews with key informants (e.g. farmers) from a certain region, area or village.
Typically, groups of key informants (knowledgeable people within a community) are brought together and interviewed by the researcher. This can be a very useful way of finding out what the people think about a subject; indeed their answers can sometimes be opposite to a researcher's expectations. It can also help with the planning of an experiment, a survey or observational study or complement the information gained from an existing survey (see Case Study 1 and Case Study 16).
A study should be planned to meet some of the goals and objectives that have been developed during the preparation of the research strategy. As already discussed under Research strategy, clearly written objectives are essential for proper planning. It is through these objectives that null hypotheses are formulated for testing. The aim of study design is to plan a study that not only meets these objectives but has realistic prospects for concluding whether a null hypothesis can be rejected or not.
Some researchers have difficulty in defining clear and concise study objectives.
Key to the planning of an experiment are the choices of treatments and the numbers of experimental units or subjects to which they are to be applied. Of equal importance is the type of environment in which an experiment is to be conducted, whether, say, on farm or on station, and whether the experiment needs to be replicated in different locations.
The goals for a survey must be clearly set out in the same way as for an experiment and be seen to fit the overall strategy. Decisions are necessary on the scope of the survey, its size in terms of numbers of questions to be asked, and its breadth in terms of areas to be sampled. Similar considerations are needed in the design of an observational study.
Careful consideration of the variability to be expected in an experiment may help to reduce 'experimental error'. This is usually achieved by 'blocking' units before they are assigned to treatment. The term 'blocking' is conventionally applied to experimental situations, that of 'stratification' to surveys. There are subtle differences in definition, discussed later, but careful stratification of a region, which is to be studied, into more homogeneous areas can produce more precise regional estimates. Likewise, by taking into account the way that land slopes when designing a field experiment, and defining 'blocks' accordingly, residual error can be reduced.
Choices of the measurements to be made and the frequencies with which they can be done also need to be addressed during the planning phase. These will include the primary measurements that are key to fulfilling the objectives, such as crop yield, animal growth, disease incidence, farmer rating, and the secondary measurements that help to explain some of the uncontrolled variation in the primary variables, perhaps season, rainfall, initial body weight, sex, age, different elements of farmer practice, and so on.
Measurements can take the form of 'continuous' variables where any reasonable value within a range is possible, or 'discrete' variables (for example, yes/no answers or a series of ranked values). Sample sizes for discrete data generally need to be greater than for continuous data in order to satisfactorily answer a hypothesis.
Close attention also needs to be paid to sample size and to what extent this may be constrained by limitations imposed by the study, e.g. capacity to handle analyses in the laboratory, numbers of farmers willing to participate in a trial, manpower available for conducting a survey, etc. Such constraints may result in compromises to the original study design, e.g. reducing the number of treatments to be compared in an experiment, reducing the numbers of regions to be studied in a survey, or changing the frequency with which measurements are taken in a longitudinal, observational study.
When planning an experiment the researcher will usually wish to estimate the efficacy of a treatment such as a fertiliser, insecticide, etc. Likewise, the word 'treatment' is applicable to studies in the veterinary or human medical field, when applied, for example, to diet, drug or method of immunisation. Sometimes there may be more than one treatment to be compared.
But the statistical use of the word 'treatment' often covers other characteristics or attributes, such as variety, breed, husbandry practice, agro-ecological zone, gender-associated practice. None of these is, in any sense of the word, a treatment, though when using a computer statistical package one may be compelled to put something into the 'treatment line'.
When working on the design or reporting of a study, however, one should try where possible to use an appropriate word that describes the particular intervention, attribute or characteristic. Often one will need to use the word 'group', sometimes 'factor', to get away from the word 'treatment'. Such a word is generally more applicable, especially in surveys and observational studies when one needs to refer to such characteristics as wealth of household, type of production system, etc.
An experimental treatment is usually compared with a baseline control. In order that unbiased estimates of the efficacy of a treatment can be obtained, both the treatment and the control need to be assigned to the available experimental subjects at random.
The simplest form of experimental design is the completely randomised design, which may contain one or more treatments, factors or groups. The experimental units are assigned at random either to the 'treatments' or the controls. Case Study 13 provides an example of a completely randomised design to compare different feeding strategies for goats. Goats were allocated at random to one of the feeds. Type of feed can hardly be described as a treatment in its traditional sense. 'Feeding group' or 'feeding system' is better.
Most experiments and observational studies, and to some extent surveys too, result in some form of analysis of variance or deviance (see Statistical modelling ). It is helpful to look ahead and to sketch the framework for the structure of the analysis during the planning phase. By sketching the analysis of variance table one can see, for example, how many degrees of freedom (d.f.) are provided for estimating the residual variance.
It is important that the variance is determined with reasonable precision for poor precision reduces the chance of achieving statistical significance of comparisons between means. The proposed size of the study may result in a number of degrees of freedom that is insufficient to estimate the variance with reasonable precision (or, as depicted in Fig. 1, indeed too many!).

Fig.1 by Herbert Symonds.
In situations where the error structure becomes more complex the analysis of variance table also allows the researcher to check the layers at which different treatments or attributes need to be compared, and to see whether proposed sample sizes are adequate for each layer. By writing out the statistical model for the analysis of variance one can also make sure that different treatments or attributes can be individually estimated and that there is no confounding of factors one with another.
In its simplest form the analysis of variance separates the total variation among the experimental or sampling units into two parts: one that can be associated with the particular groupings of individuals and one that cannot. This latter portion is often referred to as the residual or error variation. At this stage all that we need to know is how the number of degrees of freedom available in the study are partitioned. For a completely randomised design with g groups the structure of the analysis of variance is as follows:
Source of variation |
d.f. |
Group |
g - 1 |
Residual (Error) |
n - g |
Total |
n - 1 |
The total number of degrees of freedom, which is the number of experimental units minus one, is partitioned between those representing groups and those that remain (residual). When the number of units assigned to each group are the same (say, r) the degrees of freedom for the residual line can alternatively be written as g(r-1).
The residual mean square or variance (also referred to as 'error mean square'), calculated as part of the analysis of variance (not shown here, but see Statistical modelling), provides a measure of the variation among observational units that cannot be controlled, i.e. the residual variation among units within each group. This constitutes the 'experimental error' or residual variation term against which the variation among group means can be compared. As already mentioned, there must be adequate degrees of freedom for the residual term to allow a reliable estimate of the variance to be calculated.
'Blocking' is a commonly used statistical term in the design of experiments. Likewise, 'stratification' is commonly used for surveys. Their use is similar but they can have slightly different meanings.
Individual subjects are often organised into blocks when planning an experiment, in other words there is a physical act in doing so. For example, a field may be divided into a number of different areas (or blocks) (see Case Study 5, Case Study 15 or Case Study 16) and treatments assigned to plots within each block. Likewise, animals may be blocked (or grouped) by body weight or age before assigning them from within a group to treatment. Alternatively an experiment may be replicated as batches in time (see, for example, Case Study 3 and Case Study 8).
The purpose of blocking is to put the experimental units together in more homogenous groups of units before assigning them to treatments, thus reducing the size of the experimental error.
Selecting sampling units for a survey can similarly be done within strata. Here a stratum may be something that is more than likely fixed in space. It could be an agro-ecological zone, an area of land at a particular altitude or an administrative district. It could be a production system or village. Households can also be blocked for the purpose of sampling, for example grouped by wealth status. In this case it makes more sense to use the word 'block' (or 'group') rather than 'stratum'.
Stratification, in the same way as blocking, can improve the precision with which estimates are obtained. But stratification can often also be used for administrative convenience in conducting a survey. Sometimes separate estimates for each stratum are required.
An experiment that includes blocking is often referred to as a randomised block design. This design was developed many years ago for agronomic experiments when the word 'block' was used to describe a piece of land that, to all extents and purposes, is homogeneous in terms of fertility or drainage.
Usually such blocks are arranged as parallel strips of land within which series of plots are laid out for the different treatments (see, for example, Case study 16). Land gradients will tend to run opposite to the direction in which the blocks are arranged. Thus, plants planted in the same block will be expected to perform more similarly than plants planted in different blocks.
As already mentioned, randomised block designs have other fields of application and the word 'block' can take sometimes take on a different connotation. As for 'treatment', the word 'block' may not always be the most suitable descriptor to use. Indeed the more general word 'group' may often be better. Thus, cows may be grouped (better than blocked) on the basis of milk yield and treatment assigned to individuals within each group.
In situations where animals are individually penned it is sometimes possible to visualise the 'block' to which an animal belongs (based say on age or previous lactation yield) only when looking at the record card pinned outside its pen.
Blocking is done to reduce the experimental or residual error, something that will happen when the variation among experimental units among blocks is greater than the variation within blocks. Assuming there to be b blocks, and equal assignment to t treatments from within blocks, the analysis of variance structure for a randomised block becomes:
Source of variation |
d.f. |
Block |
b - 1 |
Treatment |
t - 1 |
Residual |
(b - 1) (t - 1) |
Total |
n - 1 |
If blocking is successful in producing more homogeneous groups, then the residual variance will be less than if the study had been designed as a completely randomised design. Since the residual variance is normally decreased when blocking is applied, the precision with which the means for the different treatments are compared will consequently increase. Often the number of times the level of each treatment is replicated will be the same for each level (as assumed in the analysis of variance table above) but this does not necessarily have to be so.
When treatments are not equally replicated the design often becomes 'unbalanced', in the sense that the terms for treatments and blocks in a randomised block are no longer 'orthogonal'. This can make the interpretation of the statistical analysis a little more complicated, but this should not dictate how blocking is done, and it does not matter if blocks are of different sizes. Good, sensible blocking is what is important in order to account for as much of the variation among subjects as possible.
For surveys it similarly makes sense to adjust sample sizes to account for situations where the variation within certain strata or blocks may be higher than others. Likewise, there may be instances when assignments of different numbers of experimental units to a treatment are warranted. Thus, whilst simplicity of analysis by ensuring equal replication may be desirable, the researcher should not be constrained to making blocks or strata necessarily of equal size.
When a design is unbalanced the variations attributable to the factors under investigation and the blocks to which they have been assigned tend to overlap. Thus, if a treatment is compared with a control and the two means are calculated ignoring the blocks to which individual units belong (i.e. assuming a completely randomised design), then any effect of block will be hidden within the two means. Thus, the comparison will be biased and the effect of treatment can be said to be 'partially confounded' with block. A good example of this is in the comparison of sheep breeds in Case Study 3.
Complete confounding occurs when the variation for two sources of variation cannot be distinguished one from another. Thus, if one level of a factor is set out in one stratum and a second level in a second stratum, it will be impossible to distinguish between the variation associated with the level of the factor and the stratum in which it is found. For example, the relative efficacy of a vaccine when applied to two breeds of cattle cannot be determined if each breed is evaluated in a separate experiment. Breeds need to be tested simultaneously in the same study if direct comparisons are to be made.
If the required numbers of animals are impossible to manage simultaneously, then the experiment can be replicated. The two experiments can then be considered as separate blocks (or strata) of a randomised block experiment with the two batches of animals forming the two strata. Case Study 8, which describes a feeding experiment with goats, was divided into three batches over time because it was not possible to find sufficient goats kidding at the same time. These batches are considered as blocks in the analysis.
Stratification is important in surveys. When a survey is being planned the units to be selected for sampling from a population, for example, households, can be selected from different strata according to a particular characteristic, such as agro-ecological zone, farming system, population density, household wealth, etc. These strata are chosen suspecting that the variation among sampling units within strata is smaller than that among strata (see Case Study 11), but also to facilitate the conduct of the survey. Effective stratification can reduce the total number of units that need to be sampled.
A schematic representation of how stratified sampling is done is shown below.

More than one attribute may be used at the same time for blocking or stratification, but care should be taken not to use too many attributes at the same time. For instance, there tends to be a belief among some animal researchers that groups of animals used for the different treatments must be balanced in every respect for such attributes as age, sex, breed, body weight, etc. The problem is that any semblance of randomisation becomes lost with the result that the residual degrees of freedom in the analysis of variance will tend to vanish.
This must not be allowed to happen. Instead, the one or two attributes that are considered most likely to influence the primary measurement of interest should be used in a way that ensures that there remain a reasonable number of residual degrees of freedom for estimating the residual variance. Attributes that may be suitable candidates for stratification in animal experiments are age, sex, twin, litter, body weight, milk yield, breed or sire.
Likewise in surveys there can be a tendency to use a number of attributes to 'balance' the selection of areas for sampling. These could be, for example, agro-ecological zone, altitude, livestock density, proximity to an urban area etc (see Case Study 11). This will tend to result in a representative selection of areas rather than a random sample. The researcher needs to be aware of the consequences of selecting such a sample.
Whilst sensible blocking is very important it is also possible to collect additional information to be used as covariates in the analysis (see Statistical modelling). Thus, it may be possible to block on the basis of breed and sex in an animal experiment and ignore other attributes such as age or weight. Such attributes can nevertheless be used as covariates and so should also be recorded. The art in the design of such studies is to select the appropriate attributes to use for blocking and those to be recorded for possible use as covariates.
Stratification is also an appropriate tool for use in on-farm studies. Although attributes such as farm size, sub-location etc. may not account for much of the among farm variation, it is nevertheless desirable to demonstrate that such attributes have been considered in the study design in order to demonstrate that inferences are being made without bias.
It can be common for pilot or 'look-see' experiments to be undertaken first to see whether preliminary results look promising. Such an approach needs to be considered carefully. It is perhaps most useful to envisage a pilot study as a possible first replicate 'in time' of a larger experiment. The danger of doing a pilot experiment on its own without possibilities for later extension is that it may be either too small to deduce anything or else yield data that tend to be over-interpreted by the researcher.
Experimental units are the individual subjects in an experiment assigned to a treatment or factor and on which measurements are to be made (but also see Clustering), for example, a tree, a leaf, an experimental plot, a cow, a household, a farmer's field, a patient in a clinical trial, a group of animals in a pen, a tissue culture dish, a blood sample from an animal or human being.
Subjects used in a survey are often referred to as sampling units (e.g. Case Study 11), and, in an observational study, as observational units. One can also talk of units of measurement but these may sometimes be different from experimental, observational or sampling units (see below). Experimental, observational and sampling units can thus be considered to be different expressions of the same concept but used in different settings.
There may be different types of experimental, sampling or observational units within the same study design, and observations may be measured on more than one type of unit. Thus, in an agro-forestry experiment a tree may be randomly assigned to one form of treatment and selected leaves from the tree to another. Such an experimental design is often described as a 'split-plot' design. This term was first used for agronomical experiments, in which larger plots in an experimental field were used for certain treatments (e.g. method of spraying that could only be applied to a comparatively large area), and with each of these plots subdivided into smaller plots (sub-plots) to which other treatments (e.g. level of fertiliser) could be applied.
Similarly, summary household data may be collected in a survey of households, but data may also be recorded about the individuals within the household. For example, Case Study 11 describes how certain data, such as livestock numbers, are recorded at the homestead level, but other data, such as different activities performed by different members of the homestead (men, women, boys and girls) in relationship to the management/keeping of cattle, are collected at the person category level within the homestead.
It is important to appreciate that an experimental unit may not always be the unit on which a measurement is taken. For instance, consider an experiment in which animals are randomly assigned to treatment and blood samples are taken at regular intervals for measuring, say, blood glucose. Glucose concentration is measured, of course, on the blood sample itself and, strictly speaking, not on the animal. However, since the animal is the experimental unit assigned to treatment, this becomes, in the statistical sense, the unit of 'measurement' for comparison at the animal level.
It is also important to understand at the study design stage how observations are to be used in the statistical analysis phase. In group-fed animal experiments, for example, researchers sometimes fail to appreciate that animals cannot be analysed as individual, independent observations for attributes such as weight gain (see Case Study 17). It is the groups of animals given different treatments that constitute the experimental units for treatment comparisons.
Randomisation is important because it rules out possible bias in a researcher's allocation of experimental units to treatments or choice of sampling units for a survey. Application of analysis of variance assumes independence and randomisation of the experimental or sampling units. The assumption of randomisation is essential, therefore, for ensuring that appropriate inferences can be drawn from a study. Without randomisation, experimental units cannot, in the statistical sense, be considered truly independent and to have been selected without bias.
Randomisation can be done using computerised, randomisation routines, tables of random numbers, cutting up bits of paper, using a dice etc. Whichever method is used it is important to ensure that when treatments are assigned to individuals in an experiment each individual within a block has the same chance of being selected for any of the treatments.
Procedures, which can be random, can also be used to select sub-samples of an experimental unit when it may be unnecessary to sample the whole unit. For instance, when collecting material from an agronomic experiment it may not be necessary or desirable to harvest the whole plot. Selection of individual plants may be sufficient and it may be decided to select plants at random (although this should not always be as difficult as depicted in Fig. 2!).

Fig.2. by Herbert Symonds
Alternatively, specific rules for plant selection can be drawn up to ensure that selected plants are sufficiently representative of the plot within which they are growing. This is illustrated in Case Study 16 in which only a middle selection of plants from plots are harvested. Randomisation is not necessary for this purpose because the selected plants are chosen to be as representative and homogeneous as possible (i.e. not associated with any influences at the plot margins) of the plot itself. Each plot was, of course, randomly allocated to a given Taro variety and fertiliser level, and this is the important thing.
Representative sampling is used when units or sub-units (plants in the above example) need to be selected to be representative of the sub-population being sampled. Representative sampling can often be used in surveys (see Case Study 11) when it is felt that a randomly selected sample may miss areas that may be important for inclusion and thus fail to ensure a representative coverage of a region. A degree of representative selection may be preferred particularly at the upper administrative layers. It is important though to recognise that this method of selection can influence the interpretation of the results and may introduce some degree of bias.
Subsets of experimental units may be also selected at random for specific measurements that may be expensive or time consuming to measure. Thus, for animals under experimentation blood samples may be taken from all animals for those measurements that are analytically easy to do, but from fewer for those that are analytically time-consuming or expensive. Of course, the researcher will need to verify that adequate replication is retained in the latter case.
Strict randomisation may not always be possible in surveys or observational studies, e.g. Case Study 1, Case Study 2 and Case Study 11. Often there may be good reasons for not doing so. For example, the selection of herds for monitoring milk production of Ankole cattle in Case Study 2 was influenced by ease of access by the enumerators. The assumption has been made in the statistical analysis that the samples of herds that have been selected are representative of all the herds in the respective regions and hence, for sake of argument, that the herds can be considered to be a random selection. When designing such a study the researcher needs to decide whether such an assumption is warranted or not.
Repeated sampling from an individual plot or animal cannot be strictly random in time, nor can samples, especially if they are taken close together, necessarily be considered independent of each other. Statistical analysis of such data does usually assume, however, that samples are 'random'. There are special 'repeated measures' methods available (discussed in Statistical modelling) to take into account any lack of independence.
When samples are drawn at random within a survey, it is assumed that every potential unit within the stratum, e.g. village, homestead, field etc., has an equal chance of being selected. However, when working in a village it may not be that easy to have a table of random numbers at hand and an alternative pseudo-randomisation system may need to be devised.
One solution is to make a series of random trajectories across the village, and, by walking along them, select, say, every fifth household until the required number of households is obtained. There is reasonable justification for assuming such a sample to be random. Further up the hierarchy (for example, at the district level) it may be possible to be more rigorous in ensuring that sampling units are selected truly at random when required
There are two other forms of sampling. One is 'convenience sampling'. This is used to ensure ease of access or to make best use of available manpower when conducting a survey or observational study. Thus, those herds that were within easy reach of a cycle ride were selected for monitoring in Case Study 2. This may produce a sample that may not truly randomly reflect the sub-population being studied, but may be necessary to make efficient use of available resources or to minimise the time for conducting the study.
Another method that may often be used in surveys is that of 'purposive sampling'. Here, the selection of sampling units is based, for instance, on knowledge of known farming systems or, in the case of livestock, known breed status. It may be considered important to include such a sample within a study to ensure, for instance, that a particular indigenous breed known to occur in a small area is captured. This is different from the need to ensure a representative sample. In this case data collected on the particular indigenous breed may need to be analysed separately from the other data.
In summary, each of these different methods of sampling, namely random, representative, convenience and purposive, may feature within study design. As far as possible samples should be drawn at random to ensure that sample estimates can be extrapolated to the sub-population that they represent. It should be recognised, however, that other considerations may sometimes feature. The art is in deciding on what implications different methods of sampling have on the final inferences to be drawn.
The conventional randomised block has r blocks with each treatment occurring once in each block. On the other hand, as indicated earlier, it is permissible for each treatment to occur more than once in each block, indeed with unequal replication. If a treatment occurs twice in each block then the overall replication is 2r.
The number of replicates chosen for an experiment will be the number that is required to provide a reasonable chance of detecting as significant the predetermined, expected effect of treatment. Replication should also be sufficient to provide a reasonable number of degrees of freedom for the residual line in the analysis of variance in order to provide a satisfactory estimate of the residual mean square. The fewer the degrees of freedom the less reliable is the residual variance as an estimate of the true 'population' variance.
Consider, for example, a 'randomised block' design with two breeds compared in two years with one animal used for each breed in each year. This results in a total of only four experimental units. This experiment is obviously useless. Although two animals are used for each treatment, only one residual degree of freedom remains for the error term.
As a general rule of thumb there should be between at least six to ten degrees of freedom planned for the residual term. By choosing the upper value one can allow for lost information (in the form of missing values) not spoiling the analysis. In order to achieve these numbers of degrees of freedom in the above example at least three sheep will need to be included each year for each breed. This will result in nine degrees of freedom for the residual term, although one of these can be taken up by an interaction term (see table below) which measures the extent to which differences in mean values between breeds are influenced by year.
Source of variation |
d.f. |
Breed |
1 |
Year |
1 |
Breed x Year |
1 |
Residual |
8 |
Total |
11 |
Even this replication may be too little. The number of replicates will depend primarily on the difference in mean values between breeds that the researcher desires to be judged as 'significant'. This will depend on the size of the residual variance. This is discussed later under How large should the study be?
Replicates may, or may not be, synonymous with blocks or strata. Thus one can talk of a randomised block having three blocks or three replicates. Both alternatives have the same meaning. However, a treatment may be replicated more than once in a block. In this case there is no further blocking or stratification. Similarly in a completely randomised design one can refer to each treatment being replicated a number of times. Again no blocking is involved.
Replication of sampling over time, for example when an animal is sampled repeatedly over a number of days, can be considered as a form of blocking or stratification. Several animals sampled over the same period of days will share the same day-to-day variation. Thus, day of measurement will take on the role of a replicate or block.
Plant or animal genetic studies often feature studies in which experimental units occur in 'clusters'. These designs are sometimes described as 'nested' or 'hierarchical' designs. The emphasis in these studies tends to be as much on the estimation of variances at each layer as on the estimation of group means.
As for the split-plot design mentioned under Experimental, observation or sampling units?, experimental units occur at a number of layers. Thus, in an animal genetics experiment the experimental units at the top layer may be associated with differences among sires (e.g. bulls), those at the next layer with differences among offspring within sires, and those at the bottom layer with repeated measurements made on the same offspring. A simple example, with s sires, m offspring per sire and r repeated measurements per offspring, results in the following form of analysis of variance:
Source of variation |
d.f. |
Sire |
s-1 |
Offspring/sire |
s(m-1) |
Residual (repeats) |
sm(r-1) |
Total |
smr-1 |
The sire forms the head of a cluster. Each sire has a cluster of offspring and each offspring a cluster of measurements. The residual line represents the variation among the repeated measurements at the lowest layer. The precision with which a sire mean value is estimated will depend on the numbers of offspring and also the numbers of measurements made on each offspring. For instance, the weighing of a calf on consecutive days to provide two replicates for weight provides a more precise estimate of the calf's weight than if only one measurement is taken.
Where multiple births may be common, in sheep for instance, an experiment can be designed using twins. In this case the 'offspring within sire line' in the analysis of variance can be separated into ewe (dam) within ram (sire) and lamb within ewe to provide four experimental layers. When a measurement is made on a lamb, the 'ewe' term is synonymous with 'twin', i.e. the mean of the measurements on the ewe's two lambs, and 'ram' the mean of all measurements made on lambs born to the ewes to which the ram may have been mated. The point is that even though no measurements are made on rams or ewes, the ewe still represents the experimental or observational unit to be used for sire comparisons. This point is also made under Experimental, observational or sampling units?.
Thus, although there may be several cluster layers in a study, measurements may not be taken at all layers. In designing such a study it is important, therefore, to visualise how the data will be analysed. Case Study 2 incorporates a clustered design often referred to as a nested or hierarchical design. The study was designed to assess the milking performance of village Ankole cattle in Uganda. Eight different sites, a number of herds within each site and a number of lactating cows within each herd were selected. Although measurements were also made at the farm level to asses farming practices (not shown in the case study), the measurements used for the hierarchical analysis of variance (site/herd/cow) for milk offtake were made at the animal level.
A survey invariably involves some form of hierarchical clustering. In the conduct of a survey it will often be too time-consuming to visit sampling units randomly spread across a wide area. The alternative is to devise a sampling frame which allows groups of sampling units to be visited within smaller areas. A group could be a village, a household a herd, a field and so on.
A hierarchical system is based on different layers. The top layer of the cluster might be a 'province' or the highest administrative unit in a country or a region. The next layers downwards may be 'district', then a 'sub-district', then a village. In the clustering scheme a sample of districts may be selected from a province, a sample of sub-districts then selected from the selected districts, and a sample of villages selected from the selected sub-districts. This scheme was adopted in Swaziland (see Case Study 11) for a livestock breed survey.
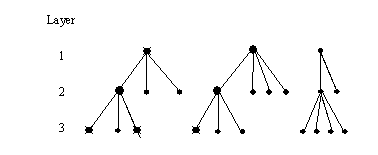
The following diagram illustrates the process of hierarchical sample selection for three layers of a structure. At the top layer there are, for the purposes of illustration, three administrative units in which two (large dots) are selected. From these units a sample of sub-units (say one each) is selected at the next layer down. At the third layer another set of samples of sub-units is selected from the range of units. The usefulness of such a design is that it focuses attention on clusters of sampling units that are easier to reach by the field study teams, and hence reduce both the time involved in conducting a survey and the costs of its execution.

Hierarchical or nested designs can be used too in laboratory experiments. For example, an assessment of a new experimental assay could be repeated over several days and with multiple measurements made on the same day. This will provide estimates of among- and within-day variation. These ideas are incorporated in Case Study 9 which determines how many microscopic readings are needed for assessing pollen grain germination of different flower buds from a Sesbania sesban (L) Merr tree used in agro-forestry systems.
Another way of looking at this case study is to consider that there are multiple levels of units, first at the tree level (selection of six buds), then at the bud level (sub-division of a bud to allow simultaneous assays at different sucrose levels), and finally at the microscopic slide level (replication of counting in 25 different fields of view). Although data are only recorded at the ultimate level, the main comparisons are made at the sucrose concentration level, each based on 6x25 measurements.
Treatments or factors and methods of blocking can be added to a hierarchical structure. Thus, sucrose concentration is a 'treatment' in Case Study 9 superimposed on the hierarchical structure of bud replication within bud size, variation between different observations made on the same bud, and variations among repeated microscopic field of view measurements for each observation.
Another example is illustrated in Case Study 4, in which effects of year of birth, breed, sex, age at weaning and age of ewe are superimposed on the two-stage hierarchical structure of ram x ewe and lamb within ram x ewe. An important point to understand is how factors are allocated to the different layers. This is taken up further in Statistical modelling.
Before a study can be contemplated some measure of its size and level of replication needs to be determined. The formula that is commonly used is:
n = 2s2 t2 / d2
where n is the required number of experimental units for each level of the factor to be compared, s2 is an estimate of the residual variance (see Exploration & description), t is the value of the Student t-test at the required level of significance (say, P=0.05 or P=0.01), and d is the difference between the two mean responses that needs to be shown to be statistically significant.
For example, a researcher planning a sheep nutrition experiment may consider it important, for a feed he/she is evaluating, to achieve an extra 0.5 kg in lamb weaning weight feeding for it to be any practical benefit compared with a standard method of feeding. Thus, d = 0.5 in the above equation.
The estimated variance s2 is often difficult to determine. Sometimes results of previous similar experiments are available. If not, a value of the likely coefficient of variation (see Exploration & description) can be taken into account. Having defined a suitable value for s2, and provided the expected response in mean weaning weight required, a value for n can be obtained. A value of 2 can be substituted in the first instance as an approximation for t for P=0.05, and a value of 2.6 for P=0.01.
If a calculated value of n seems reasonable to the researcher, then an iterative procedure for refining the required sample size can be initiated as illustrated in Case Study 8. This is not usually necessary in practice because sampling variances will vary from one experiment to another, and the researcher needs only to choose a reasonable value for n, based on the estimates given. He/she will also appreciate that the larger the sample size he/she chooses the more powerful the experiment will be for evaluating the null hypothesis.
The question of sample size is also addressed in Case Study 9. The results of the experiment are analysed in a way that allow a subsequent experimental protocol to be prepared having gained a knowledge of the variations that occur in germination rates among and within buds and among microscopic fields of view.
Often the value of n will result in a study that is too large to handle. Various options can then be considered. The impact of introducing lower estimates of s2 into the formula might be considered. Alternatively, the expected response to the treatment or the expected influence of an attribute under investigation can be reconsidered. Perhaps the study can be simplified by reducing the number of treatments to be compared. Or maybe the study can be arranged to be replicated in batches over time. These various options need to be discussed between the researcher and biometrician.
The process of determining optimal sample size can often lead the researcher to rethink the original objectives and corresponding hypotheses. Often a compromise needs to be made between what is desirable in terms of numbers of units from a statistical point of view, and the number of units that can be handled. This may depend on available facilities and resources or, even sometimes, level of funding.
Researchers need to appreciate the likely impact of a compromised solution on the success of an experiment, and when to abandon the idea altogether (see Case Study 8). There is no point in undertaking an experiment for which a sample size is deemed to be so small that subsequent statistical analysis is unlikely to yield anything useful. In larger field trials where a statistically significant result may be difficult to achieve, it must be clear from the outset what result is expected and how the study fits into the overall research strategy.
The precision which an estimated mean value can be determined is given by its 'standard error' ![]() . A reduction in the standard error can be achieved by increasing n or reducing s2. Effective use of stratification or selecting homogeneous units can reduce s2. This is one of the keys to good study design.
. A reduction in the standard error can be achieved by increasing n or reducing s2. Effective use of stratification or selecting homogeneous units can reduce s2. This is one of the keys to good study design.
Similar considerations need to be applied in selecting a suitable sample size for surveys. As for designed experiments this is based on the precision with which population estimates need to be determined. If population estimation is not the main purpose for a survey, then other considerations will determine an appropriate sample size.
The formula used for a standard error of an estimated mean is slightly different for a survey than for an experiment. It is:
where n is the number of sampling units, N the number of population units from which the sample is drawn (for example the number of households in a village) and s2 the variance among the sampling units.
The 'population' from which a sample of units is drawn from an experiment, and hence assumed to represent, is generally considered to be infinite. As N tends to infinity the above formula converges to ![]() , the formula already used for an experiment. When conducting an experiment the researcher generally has no perception of a fixed population size.
, the formula already used for an experiment. When conducting an experiment the researcher generally has no perception of a fixed population size.
As in experiments the researcher needs to have some knowledge of the level of variation to expect in a survey. This knowledge might be acquired from previous surveys. The value of s2 can also be reduced by effective stratification. The formula above also requires knowledge of N. This will generally be known at the upper administrative layers but not necessarily at the village layer. Before sampling a village, therefore, it may be necessary to visit the village beforehand to ascertain the number of households in the village.
If N is known for each administrative unit at each layer, the most efficient method of sampling is to sample in proportion to the number of units available for sampling. Thus, if two villages have been selected, one with N1 households and one with N2 households, the optimal distribution of n households to be sampled is such that n1/N1= n2/N2 where n1 + n2 = n. If N1 and N2 are unknown at the planning stage then it is likely to be most convenient to divide the sample equally between the villages.
Typically, the fraction (or proportion) of units that needs to be sampled from a population for the purposes of population estimation falls within the range of 0.1 to 1% of the total number of units in the population. The desired fraction, however, will depend on the objectives of the survey and the precision with which s2 can be determined.
Surveys will normally involve several sets of observations or measurements being collected for different variables, e.g. numbers of members in the household, numbers of livestock, farm size, housing of livestock, and so on. Some measurements may be more variable than others and the researcher will need to decide whether increased replication is needed for such variables. The researcher should also prioritise the important variables and ensure that the survey is large enough to estimate mean values for those variables within the required levels of precision.
Discrete responses (e.g. housing/no housing, alive/dead) and other forms of categorical data generally require larger sample sizes to achieve the same level of precision achieved by continuous variables. Such considerations also apply for experiments. Sub-surveys can be planned within the main survey itself if extra focus is required on certain variables.
Generally the variation among experimental or sampling units increases as one moves up the cluster hierarchy. Thus, variations among sub-districts will be greater than variations among villages, which in turn will be greater than variations among household within villages. Similarly within the experimental environment the variations in an animal's blood glucose from day to day will generally be less than the variation in mean blood glucose from animal to animal.
Case Study 9 illustrates the variation in germination rates among and within repeated microscopic field of view readings and shows that the variation across field of view readings in a slide is much less than the variation across slides.
When the researcher is interested in estimating the effects of two sets of treatments or factors he/she should ideally do this within the same study. This is a particularly powerful approach because it provides efficient uses of resources and, at the same time, allows the researcher to determine whether pairs of factors are additive in their effects or whether they interact in some way. Case Study 13, Case Study 15 and Case Study 16 each provide examples of factorial experiments.
A randomised block experiment with equal replication and two factors A (a levels) and B (b levels) produces the following analysis of variance structure:
Source of variation |
d.f. |
Blocks |
r-1 |
A |
a-1 |
B |
b-1 |
A x B |
(a-1) (b-1) |
Residual |
(r-1) (ab-1) |
Total |
abr-1 |
If the A x B interaction is non-significant then the effects of factors A and B can be considered to be independent and additive one to another
To demonstrate the power of a factorial design consider a 2 x 2 factorial experiment with each treatment (factor) combination, i.e. A1, A2, B1 and B2, replicated three times in three blocks.
Block |
Factor assignment | |||
1 |
A1B1 |
A2B1 |
A2B2 |
A1B2 |
2 |
A2B2 |
A2B1 |
A1B2 |
A1B1 |
3 |
A1B1 |
A2B2 |
A1B2 |
A2B1 |
Thus, each factor level, (A1, for example), is replicated three times at both levels of the other factor, (namely B1 and B2).
When there is no significant interaction between A and B, each factor can be considered to act independently of the other. This means that similar differences between A1 and A2 are observed at both levels of B. It follows that A1 and A2 can be compared by averaging over both B1 and B2, i.e. with six replicates, double the number if A1 and A2 were studied separately. A study that simultaneously involves more than one factor is, therefore, more efficient than separate studies undertaken for each factor.
Factorial experiments also get over the problem of confounding. For example, if a vaccination strategy is to be compared on indigenous and exotic breeds of cattle, it is much better to consider its effect when both breeds are studied together in the single experiment (breed then takes on the role of a factor) than when breeds are used in two experiments, one for each breed. The second approach cannot disassociate breed from experimental environment or different period.
Factorial designs can also be applied in observational studies. An example can be found in human medicine where children of different ages are recruited in case/control studies for different types of malaria. Here characteristics found in individuals that develop either cerebral or severe malaria (two known conditions of malaria) - the first factor - can be compared across age groups - the second factor.
One may also need to be careful about the possibilities of confounding in observational studies. For example, comparisons of the performance of different breeds of cattle cannot be made if they live in different areas.
Factorial experiments can be designed with more than two levels for each factor (for example, Case Study 13 which compares three breeds of goats fed three dietary rates), or with more than two factors (for example, Case Study 15 which compares two dry bean varieties planted at three seeding rates and with two levels of fertiliser). But as the number of factors increases it can become more difficult to accommodate the numbers of factorial combinations in one block or even in a single study. The strategies of partial confounded designs and fractional factorial designs can address these situations. A number of data sets covering a variety of agronomic factorial, incomplete, lattice and row-column designs have been provided by Harvey Dicks, University of KwaZulu Natal, in GenStat data sets.
The split-plot experiment (see Case Study 16) is a particular example of a factorial experiment. One factor occurs at the main plot layer and the second factor at the sub-plot layer. Thus, factorial structures can occur across more than one layer.
Most studies need to include some baseline against which a treatment or other factor can be assessed. This could be a standard variety against which improved varieties are to be compared. It could be a standard diet applied in a nutritional experiment against which feed supplementations are to be evaluated. As discussed in Case Study 6, it could be a group of farmers maintaining their standard feeding practices for their cows against which a 'treatment' group of farmers feeding an alternative regime can be compared.
Baseline studies can also be undertaken (see, for example, Case Study 10) to provide a reference point against which subsequent interventions might be judged.
Distinction sometimes needs to be made between 'positive' and 'negative' controls. Both may be necessary. For instance, in an animal vaccination experiment a vaccine may need to be delivered to an animal through a certain route or 'medium'. This 'medium', when used alone, may also offer some form of protection. Thus, vaccine experiments may typically include three 'treatments' - the vaccine to be evaluated, a 'placebo' or non-treatment (a positive control), and no treatment (a negative control). The negative control is important to determine the level of infection, and the positive control to rule out any effect of the route of delivery alone without the vaccine. Once the testing of the vaccine moves to the field the need for the positive control may no longer be required.
When factorial arrangements of treatments are used the baseline control may be the treatment A1B1. In other words the baseline control is the treatment defined with A and B at their base levels. Alternatively a control treatment may be defined independently of the other factors. In this case, the A x B factorial experiment considered above could be designed to include an additional baseline control resulting in a total of ab + 1 'treatments'. Thus, for example, an experiment may be designed to investigate an animal treatment with two doses each inoculated intramuscularly or intravenously. Thus level of dose and method of inoculation represent the two factors A and B. An additional group of animals might also be used as a negative control without treatment to result in ab + 1 treatments.
Sometimes it may be impossible to include an appropriate baseline control. For instance, many smallholders will possess only one cow. 'Single cow' studies thus need some alternative form of design. One approach might be to collect ancillary data on the cow or farm that might help to explain some of the differences that might be expressed between cows living in different farms. Such a method, however, is unlikely to be effective in practice since management differences that cannot be quantified will determine the major differences among farms.
A better approach might be to monitor the cow for a while before the intervention is implemented. Such pre-trial data can be used as covariates in the statistical analysis.
Such techniques may also be useful in other studies, even those that are carefully controlled within a laboratory. Indeed, sample size can be reduced if baseline data collected prior to the study is effective in reducing among unit variation in the study itself (see for example Case Study 8 in which goats were milked for a period of 15 days before the experiment started.)
Another type of design that that can be considered within this context is the 'cross-over design'. Individual subjects are given a series of treatments in turn, one of which will be a baseline control. In this way individuals act as their own controls and treatments can be compared within rather than among animals. Such a design may be possible in 'single cow' studies.
There is no difference in principle between an experiment carried out on farm and one carried out on station or in an environmentally controlled situation. The main thing to remember is that studies carried out on farms have more variability and therefore need more care in designing them.
When setting up a field experiment using different farms it may not be possible to accommodate all treatments at each farm. The type of design would thus fall into the category of a randomised blocked design, with a farm as a block, but with not every treatment necessarily occurring within each farm. This type of design is sometimes referred to as an 'incomplete block' design.
Alternatively, it may be possible to replicate some treatments more than once at a farm. If so, it may be possible to contemplate some form of randomised block design at each farm to ensure optimal treatment replication within each farm. It may not be possible to lay plots in the same systematic way as they are done for an on-station trial , and so blocks may take various forms and shapes. Error variation will also be much greater in an on-farm situation and this will influence sample size.
Other issues, already covered, will also need to be considered. For example, where should the study be conducted and over how wide an area? Should the area be stratified? Will controls be needed? What form should they take? Should all farmers apply the same control treatment or should the control be the farmer's normal practice? How should farmers be selected for the experiment? Should they be chosen at random or selected on the basis of likely cooperativeness? Are there any additional measurements that can be taken that might be used as covariates in the statistical analysis? And so on.....
Decisions need to be taken at the planning stage as to the level of participation expected from the farmer. There are three possibilities.
An important issue when designing an on-farm study is to decide which type of study is the most appropriate and how much participation is desired. Study design will need to accommodate the increasing level of experimental error likely to occur with increasing levels of participation. Case Study 6 alludes further to the different types of farmer participation that might occur in an on-farm study.
The greater the participation of the farmer in the design and management of the study the more complex might be the analysis and the more care needed in interpreting the results. Interest will often focus more on variations in the impact of a treatment across different farms, rather than on its overall mean impact. The problems of confounding (partial or complete) too may be particularly relevant. The general principles of study design - replication, randomisation, stratification - nevertheless still apply. As for other types of studies the researcher will need to define clearly and concisely the objectives for the study, set out the null hypotheses to be evaluated and draft out a likely framework for the statistical analysis.
Sometimes farmers can be asked to participate in a study just to provide information and knowledge. Case Study 1 refers to a participatory method used to find out farmers' knowledge about the signs and causes of trypanosomosis in cattle. Careful design of the procedure to be used for extracting the information was needed, together with deciding on how many separate groups of farmers to form.
Whenever a research activity anticipates some form of farmer participation, its purpose, and the form the participation is expected to take, needs to be determined, in order that its effect on the design of a study can be assessed. Some researchers feel that if their research is to lead to ownership and adoption of new technologies by farmers then it must involve the farmers throughout the research process. This may be true at certain stages, but each study must be looked at independently; indeed, sometimes it may be preferable for the researcher to retain complete control. The choice depends on the particular objective of the study and how the results are to be utilised.
Sooner or later 'treatments' tested in on-station trials will require further evaluation in the field. This could be a method of disease control, adoption of a new crop variety, method of pesticide management or other form of farming practice.
Much that has already been discussed also applies to the planning of studies designed to test the impacts of such interventions. Such a study may involve identification of farmers willing to participate in the trial, with assignment of some farmers to the new treatment to be implemented, and some farmers requested to continue following their normal practice.
Such trials are difficult to control especially when farmer involvement is required. For instance, after a trial has been in progress for some time some of the control farmers may hear of the benefits being achieved by farmers receiving the new treatment and may want to follow suit (see Case Study 6). There may also be difficulties selecting participants at random, and this can influence the interpretation of results.
An alternative method for field testing is to apply the intervention to all farms during one or more years and compare results with previous years. This is thwart with difficulties too because any impact of the treatment may be confounded with other changes that may take place that coincide with the year(s) under investigation.
Case Study 10 illustrates a study undertaken to assess the impact of a tsetse control intervention on trypanosmosis prevalence in village cattle. Because the vector of the disease (tsetse) was prevalent over a wide area it was not possible to select control and intervention herds. The only alternative was to compare disease prevalence in a number of herds, both before and after the intervention, and to hope that monitoring could be maintained over a sufficiently long period of time to minimise any effect of other confounding factors that might influence the level of disease prevalence.
Impact assessment studies are difficult to manage but are, nevertheless, important in terms of the overall research strategy.
Decisions on what to measure or observe, how to measure and how often to measure are important considerations in study design and should be part of the planning phase. Thus, when sampling from a plot in a field experiment (see, for example, Case Study 5), questions need to be addressed on which plants to be selected for harvesting, how many to harvest and what should be measured on them. When taking repeated samples from a plot, decisions need to be taken as to when and how frequently samples should be taken.
Similarly, animal experiments can result in the collection and analysis of several samples over time. Careful choice of sampling points that focus on the strategic stages of the study (for example, when severity of disease will be at its highest or when animals are treated) can ensure efficient use of resources.
Many studies, not just surveys, involve data collected through a questionnaire. Case Study 1, a survey of dairy management practices among Orma people in Eastern Kenya, and Case Study 11, a livestock breed survey in Swaziland, provide two examples.
Having decided to embark on a survey there is often the temptation to collect as much information as possible. This temptation should be avoided. Execution of surveys and observational studies are time consuming. To add extra questions to a questionnaire not only makes interviews longer and risks the respondent becoming tired, but also requires extra time spent in analysing the answers to the questions.
The time involved in setting up a data base, entering the data and analysing them should not be underestimated. It is thus important to retain the focus of the study and ensure that, as far as possible, only those questions that meet the objectives of the study are included.
To illustrate these point further, data were collected from each farmer included within Case Study 2 (data not shown) to complement the data on milk offtakes recorded on the cows themselves. This was to provide overall background information on the production systems being applied, details of milk consumption in the households and details of quantities of milk marketed. Whilst valuable as background information some of the data that were collected did not lend themselves to analysis in the way that was anticipated. This was partly due to the somewhat small sample size at the farm data layer and partly to the methods used to collect the data. Alternative approaches to the study design might have yielded more useful data. Similar considerations apply for Case Study 1.
Questions contained in questionnaires can fall into three categories. Firstly, there is the 'closed' question in which the respondent is required to provide answers to a list of alternatives put to him/her. Opposite to this is the 'open' question which allows the respondent to answer freely and without constraint. In between there is the 'semi-open' question in which the respondent is allowed to answer freely, but with his/her answers ticked against a prescribed list not shown to him or her. A number of examples are illustrated in Case Study 11.
Closed questions may be designed to allow multiple answers to a list of alternatives, or single answers, such as yes/no. Semi-open questions that expect one of a multiple set of answers will usually have an 'other' alternative to cover answers not included within the prepared list. However, when designing a questionnaire the researcher should as far as possible ensure that the defined list of alternatives is as complete as possible so that the 'other' category is rarely used.
Careful questionnaire design is essential. Questions must be phrased in a way that ensures clear and unambiguous answers. Good questionnaire design is an art and requires practice.
Before any survey starts the questionnaire should be tested in a pilot study in order to make sure that the formats of the questions are appropriate. This provides also a good opportunity to time the length of the interview, and, if it seems too long, to see whether any questions might be omitted.
Sometimes questions require an indication of the respondent's perception to something, e.g. 'strongly agree', 'agree', 'unconcerned', 'disagree', 'strongly disagree'. Pre-testing the questionnaires allows the suitability of these alternatives to be assessed.
Various aspects of survey design and execution are discussed by Rowlands et al. (2003) in relation to the planning of livestock breed surveys in southern Africa.
Many studies, including those evaluating the adoption of interventions, will involve some form of repeated data collection. Sometimes this is needed in order to assess and understand the impact of a treatment at strategic intervals of times. Alternatively, animal deaths may need to be monitored in order to compare rates of survival. Data will also need to be collected at strategic points in time when assessing the impact of an intervention (see Case Study 10), or to indicate significant changes in the environment which may take place as a result of alterations, say, in land use.
In undertaking such monitoring a number of sampling points will need to be selected both in time and space, with the latter spread at intervals through the study area. Thus, in monitoring the prevalence of trypanasomosis in cattle within a certain locality, a number of traps could be placed at strategic points within the study area to catch and monitor at strategic times changes in the numbers of tsetse flies that transmit the disease (Case Study 10). The number of sampling points in space will depend on the likely variations to be observed across the area being studied, and the precision with which mean values need to be determined so that changes over time might achieve statistical significance.
As well as selecting a range of sampling points in space, decisions will also be needed on how frequently to sample over time. This can be overlooked in study design. There is no point in having an efficient design at the upper layers of the study for it to be spoilt by unnecessary replication over time. Monitoring points will be determined by the variability expected in time, by the strategic time points when the researcher anticipates the most significant events to occur, and the way the data are expected to be analysed.
The design of a monitoring scheme will require, not only an assessment of the numbers of units to sample, but also the frequency of sampling over time.
When an intervention is being applied without a current baseline control, and confounding with other uncontrollable factors such as changes in the weather, changes in land use, etc. are likely to occur, it is not easy to apply formal statistical tests. Sometimes a suitable range (e.g. a 3 or 4 standard deviation range) may be defined within which the mean would normally be expected to lie, so that any divergence outside these boundaries can be considered to be abnormal and hence 'significant'.
The standard deviation could be calculated from the variation among sampling units within each sampling occasion. Preliminary monitoring to assess the 'normal' variation over time will help to establish whether this is a satisfactory rule, or whether the normal range should be based on sample to sample variation during a preliminary, monitoring phase.
Monitoring for quality control purposes can also be applied within the laboratory environment. Methods for conducting scientific assays to assess biological test sample concentrations often rely on simultaneous analysis of control samples, for which concentrations are known, and against which the test sample concentrations can be compared. Should any drifts in control values not be detected, for example when a control batch is changed, faulty test results will occur.
It is important to ensure that adequate quality control is applied to maintain the control sample concentrations within tight limits to ensure that there is little drift in control values with time. The same principles described above (i.e. 3 or 4 standard deviation limits) can be applied for determining normal ranges. These can be calculated from a series of measurements during the initial assessment of the assay.
Whatever the composition of a research team, there will be a need for consultations between individual members of the team in different aspects of the research. The biometrician, or researcher offering the biometric expertise, will (or should) be called upon to advise on the design of the study. Few training courses give practice in consulting. Here we list some general points.
Throughout, both the researcher and biometrician should view study design development as a collaborative exercise, and appreciate that each needs to respect each other's particular expertise and professionalism. Practical consultation exercises should be encouraged in applied biometry courses.
Case Study 5 and Case Study 13 include experimental protocols prepared by the researchers. These could form the basis for researcher/biometrician discussions to be acted by students.
Participants who reviewed this Biometrics & Research Methods Teaching Resource at a workshop held at the University of Cape Town recommended the following text books:
Douglas C. Montgomery. 2004. Design and Analysis of Experiments. Sixth edition. John Wiley & Sons.
Hayek, Lee-Ann C. and Buzas, Martin A. 1997. Surveying Natural Populations. Columbia University Press, New York
Mead, Roger, Curnow, Robert N. and Hasted, Anne M. 2002. Statistical Methods in Agriculture and Experimental Biology. Third Edition (paperback) Chapman & Hall/CRC
Petersen R.G. 1994. Agricultural Field Experiments: Design and Analysis. Marcel Decker, New York.
Quinn, Gerry P. and Keough, Michael J. 2002. Experimental Design and Data Analysis for Biologists. Cambridge University Press.
Steel, Robert G. D., Torrie James, M and Dickey, David A.M.1996. Principles and Procedures of Statistics: A Biometrical Approach. Third edition. McGraw-Hill Companies.
In addition, relevant chapters on aspects of study design from the text book: "A First Course in Biometry for Agricultural Students" by Rayner (1967) are contained within this Teaching Resource. Course notes given by the late Harvey Dicks on "Introduction to Experimental Design" to students at the University of Natal are also to be recommended.
The reader is also referred to the Good Statistical Practice Guides on Planning written by Statistical Services Centre University of Reading:
Concepts Underlying the Design of Experiments
Guidelines for Planning Effective Surveys
On-Farm Trials - Some Biometric Guidelines